Inflation and the Timing of Actions With Discretionary Monetary Policy

The optimal (or equilibrium) inflation rate is one of the most important and most studied ideas in monetary economics. Dating back to the influential 1977 paper "Rules Rather Than Discretion: The Inconsistency of Optimal Plans" by Finn Kydland and Edward Prescott, economists have understood that a central bank's ability to commit to future policies can affect the long-run optimal inflation rate. When the central bank can commit, the long-run inflation rate can be thought of as something the central bank can choose and achieve. In contrast, when the central bank cannot commit — that is, when its promises lack credibility — the long-run inflation rate is an equilibrium outcome of the interaction between the central bank and private agents.

The case where the central bank cannot commit is sometimes referred to as the case of discretionary monetary policy, or simply discretion. A general finding from literature on the subject is that the optimal inflation rate will be higher under discretion than under commitment. Recent research has highlighted the fact that, under discretion, the timing of actions between firms and the central bank generally has implications for the nature of equilibrium, including the level of inflation. In this article, we describe how the timing of actions affects the equilibrium inflation rate in a simplified version of the standard sticky price model.

Literature on Central Bank Commitment and the Optimal Inflation Rate

Under commitment, the central bank initially chooses the entire future path of inflation, with the path depending on exogenous shocks that hit the economy. In contrast, under discretion, the central bank can only choose the current policy action each period, so the average or steady-state inflation rate depends on interaction between the private sector and the central bank. Also, under discretion, the central bank may have limited control over even the current inflation rate.

The basic issue first identified by Kydland and Prescott is that the interaction in many macroeconomic models between the central bank and the private sector leads to an inflation bias. A central bank that cannot commit — or that reneges on its commitment — has an incentive to surprise households and firms with more expansionary policy than promised under commitment. This can succeed once, but households and firms cannot be surprised in the same way repeatedly, as they come to expect higher inflation than what was promised. In equilibrium, the inflation rate will be high enough that the central bank does not have an incentive to introduce a surprise.

The timing of actions between private agents and the central bank affects the nature of equilibrium and, thus, the inflation bias when the central bank cannot commit. In our 2019 paper "Discretionary Monetary Policy in the Calvo Model" — which we'll refer to here as VW — we study the equilibrium optimal inflation rate under discretion in the popular Calvo pricing model, assuming that each period the central bank chooses the money supply before firms set their prices. The 2023 working paper "Monetary Policy Without Commitment" by Hassan Afrouzi, Marina Halac, Kenneth Rogoff and Pierre Yared — which we'll refer to here as AHRY — flips the within-period timing, so firms choose their prices before the central bank takes its action.

It turns out that this change in timing leads to a dramatic simplification in the conditions describing equilibrium. To determine the steady-state inflation rate, VW first need to solve for functions that describe dynamically optimal behavior by firms and the central bank. This is a complicated numerical problem. In contrast, AHRY show that, under the alternative timing assumption, the central bank's behavior is described by a simple static condition.

In addition to adding simplicity, changing the timing assumption also has major implications for the equilibrium inflation rate. In VW's benchmark calibration, the steady state inflation rate is 5.4 percent annually. With the alternative timing, the steady-state inflation rate for that calibration is more than 29 percent.¹

Description of Model

To gain insight into what drives this difference, we study a simplified version of the Calvo model in the rest of this article. The model is comprised of households, firms and a central bank. Households choose consumption and labor to maximize utility, taking as given wages and prices for a set of goods. Also, households must hold a quantity of money equal to their consumption.²

Firms produce using labor as an input and face a downward-sloping demand function for the goods they produce. A fraction of firms is exogenously prevented from adjusting prices. Instead, they must hire enough labor to meet the demand for their output at a predetermined price. The rest of the firms are allowed to adjust their price and choose the price that maximizes profits.

The central bank chooses the money supply to maximize the household's utility. We study a rational expectations equilibrium, where households, firms and the central bank accurately forecast or observe prices and quantities. Depending on the timing assumption, firms will adjust their prices having observed the money supply (VW), or the central bank will choose the money supply having observed prices (AHRY).

The difference between the model studied here and the Calvo model in VW and AHRY is that the model here has only one period. For firms that can adjust their prices, they maximize current period profits instead of the present discounted value of profits. One can also view the model as a special case of the multiperiod model where the subjective discount factor is set to zero.

Distortions and Inflation

The model features two distortions relative to a purely frictionless, competitive world: a relative price distortion and a markup distortion.

Relative Price Distortion

Each firm uses the same technology, and each firm's output is valued identically by consumers, who nonetheless prefer variety. Because of these assumptions, it would be optimal for the price charged by each firm to be identical so that each firm produces the same quantity and consumers consume the same quantity of each good. If there is price dispersion across firms, consumers could be made better off by a reallocation of input from low-price firms to high-price firms. Price dispersion effectively reduces aggregate productivity, an effect that is measured by the relative price distortion.

Markup Distortion

The model features monopolistic competition, and the average markup is a measure of the distortion that comes from monopoly power. Each firm faces the same marginal cost, but their markups differ because their prices differ.

Dependence on the Inflation Rate

Both the relative price distortion and the markup distortion depend on the inflation rate. Inflation is an outcome of firms' pricing decisions, and those decisions are in turn influenced by monetary policy. One way to view the monetary policy problem is that it attempts to minimize an appropriately weighted average of the markup and relative price distortions. The appropriate weights depend on how the markup and the relative price distortion influence households' utility from consumption and leisure.

Equilibrium When the Central Bank Moves First

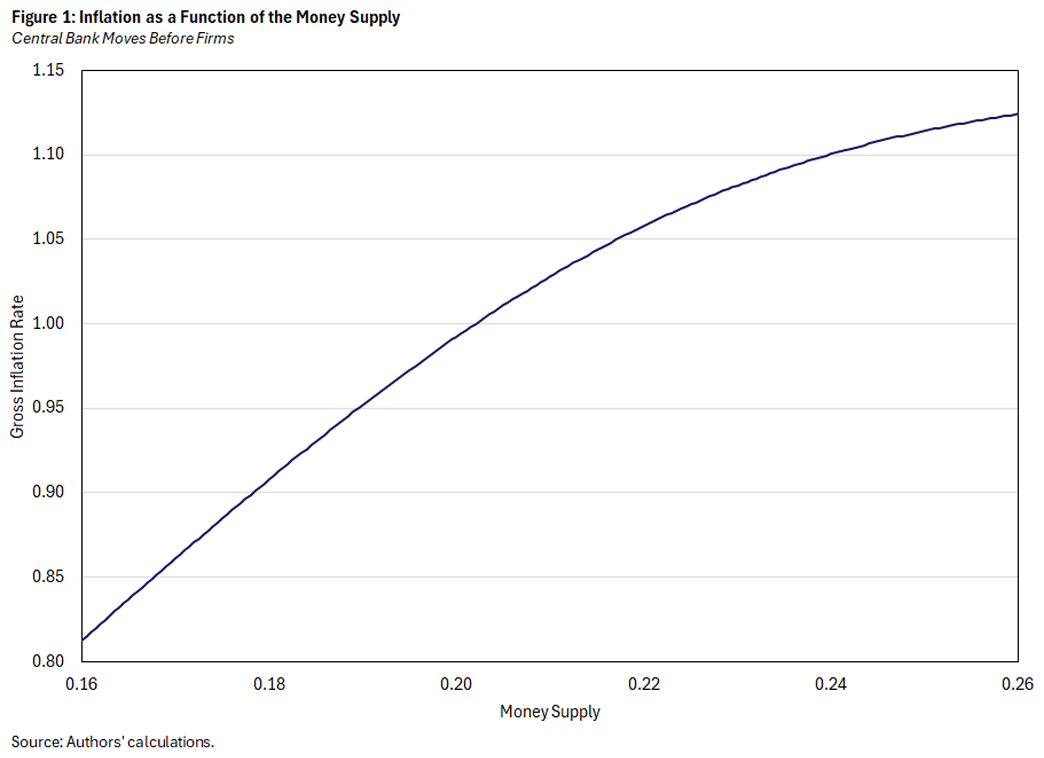
At the beginning of the period, regardless of the timing assumption, all goods have a price that the firm charged in the previous period. For simplicity, we assume that this price is identical across all firms. Under VW timing, the central bank chooses the money supply, and then those firms that are allowed to do so adjust their prices. The central bank understands how firms' pricing will respond to any money supply that it chooses, and it incorporates that response when it evaluates households' utility associated with different levels of the money supply. Firms' pricing decisions determine the inflation rate, which is shown as a function of the money supply in Figure 1: A higher money supply corresponds to higher prices set by adjusting firms and, therefore, a higher inflation rate.

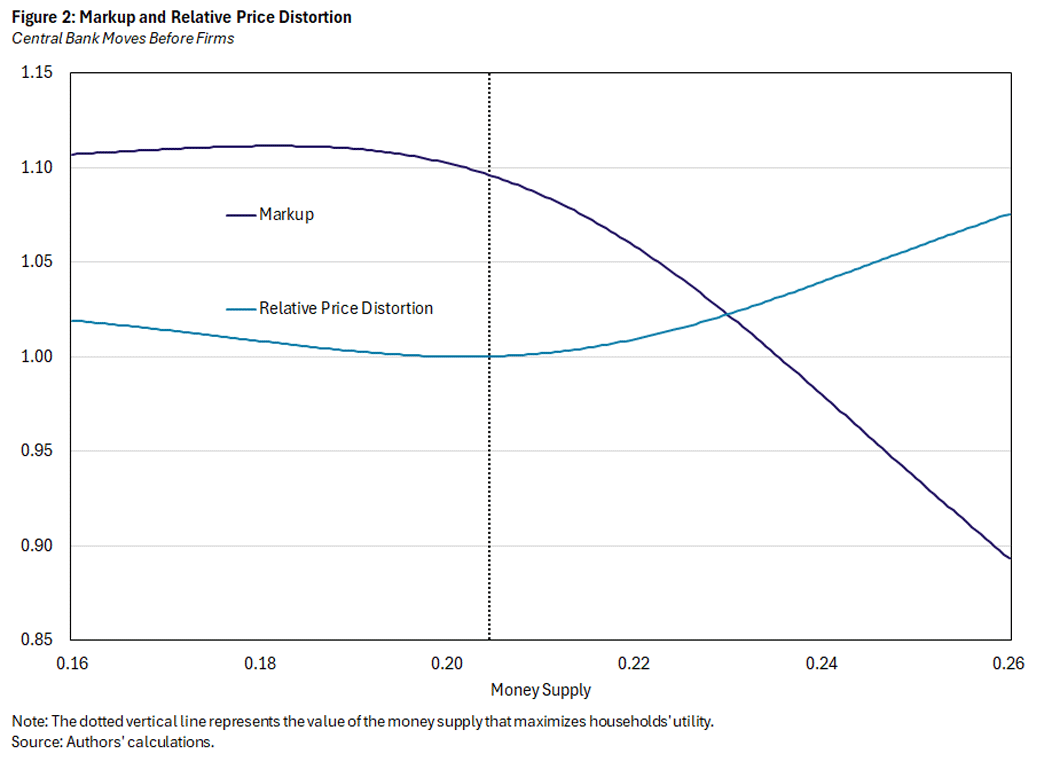
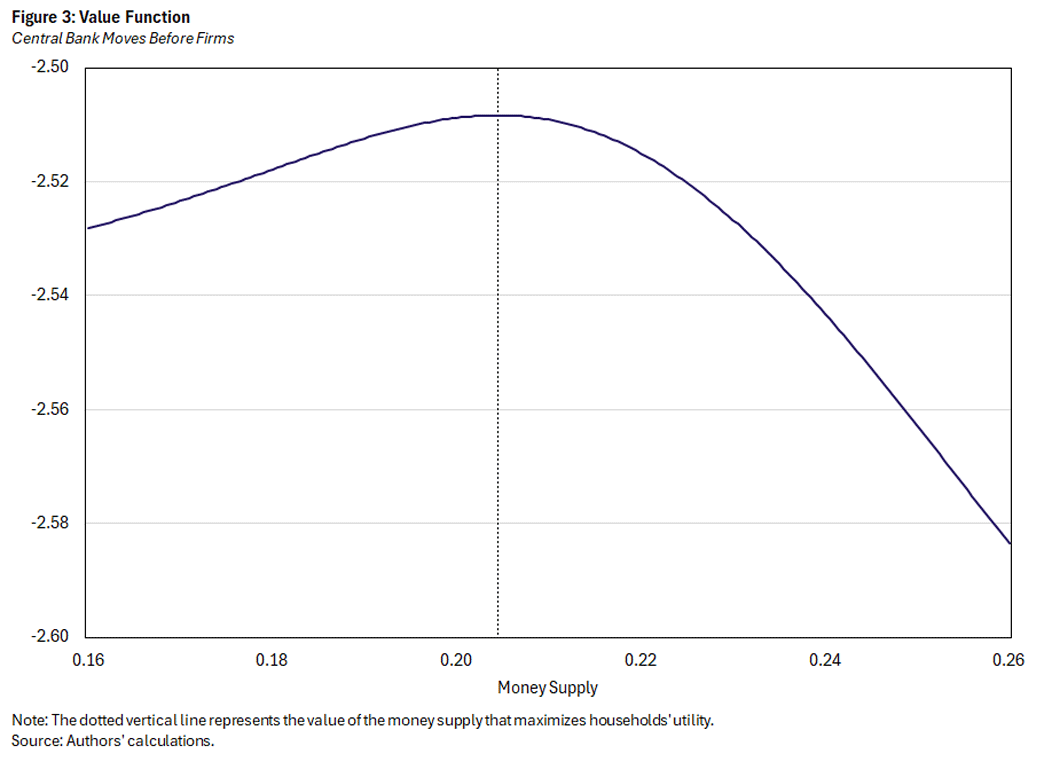
Firms' prices also determine the markup and the relative price distortion, and the central bank balances those implications. Figure 2 plots the markup and the relative price distortion for the same values of the money supply shown in Figure 1. The vertical line represents the value of the money supply that maximizes households' utility, shown in Figure 3. Note that it is feasible for the central bank to eliminate either one of the distortions (in other words, set them equal to 1) but not both: At the optimal value of the money supply, the central bank could reduce the markup further, but this would be at the cost of a higher relative price distortion.

Equilibrium When Firms Move First

Under AHRY timing, firms choose their prices, and then the central bank chooses the money supply. Thus, instead of firms reacting to the central bank's policy action, the central bank reacts to firms' pricing decisions.

It may be tempting to use the identical reasoning as above and simply flip the actors (to think that now firms incorporate the monetary policy response into their choice of what price to set). This is incorrect, because unlike the central bank, each firm is small and has no effect on aggregate variables. Firms necessarily have an expectation of the money supply level when they consider the implications of choosing different prices. However, that expectation is a fixed number, rather than something that varies with the price the firm is considering. The central bank does respond to the overall price level, but individual firms correctly believe that their action has no effect on the overall price level. In a discretionary equilibrium, the money supply that firms expect is also the money supply that the central bank chooses to maximize utility.

Reversing the timing has major implications for the central bank's problem and the nature of equilibrium. To explain this, we will refer to Figures 1-3, considering their analogues under AHRY timing. Figure 1 displayed the inflation rate as an increasing function of the money supply. Under AHRY timing, this function is flat: The inflation rate is already known when the money supply is chosen, so the central bank has no ability to change inflation by changing the money supply.³

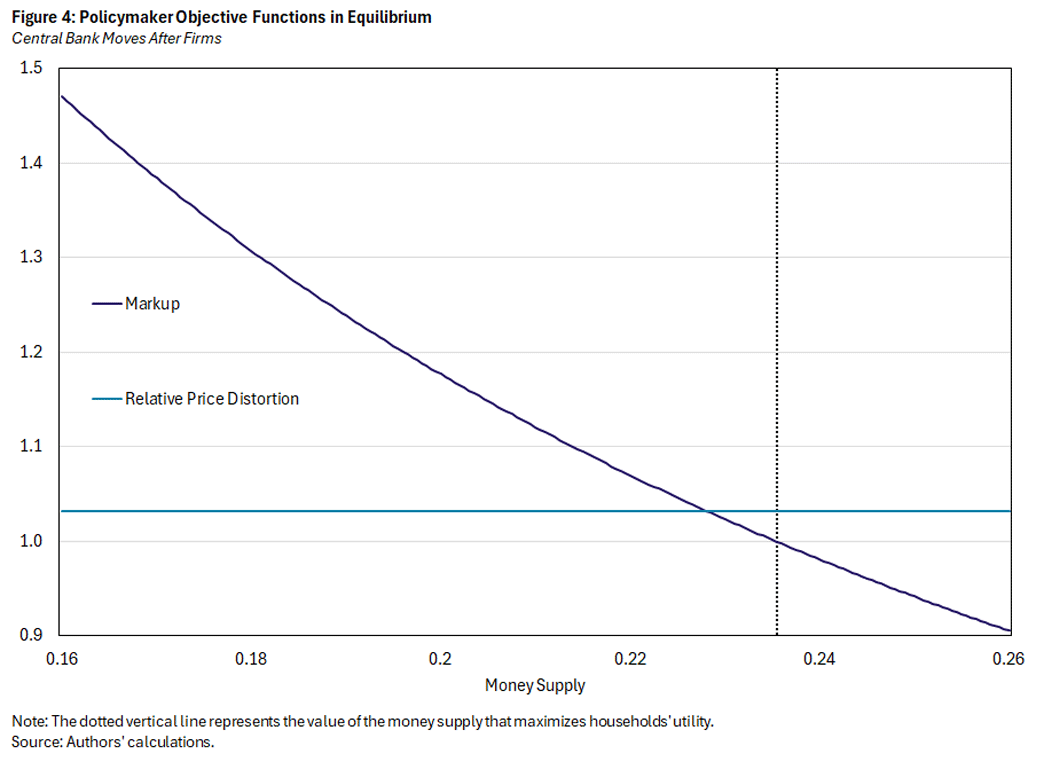
This same reasoning carries over to Figure 4, which is the analogue of Figure 2 for AHRY timing: The relative price distortion is now determined before the central bank makes its choice, so it is a flat line. However, the central bank can still affect the markup, because the money supply affects aggregate demand and, hence, marginal cost. Figure 4 highlights the key implication of changing the timing so that prices are determined before the money supply: The central bank no longer faces a trade-off between the markup and the relative price distortion, so it chooses the money supply to eliminate the markup. The vertical line in Figure 4 is the utility maximizing level of the money supply, and it occurs at a level of m such that the gross markup is 1.0 (that is, there is no markup).

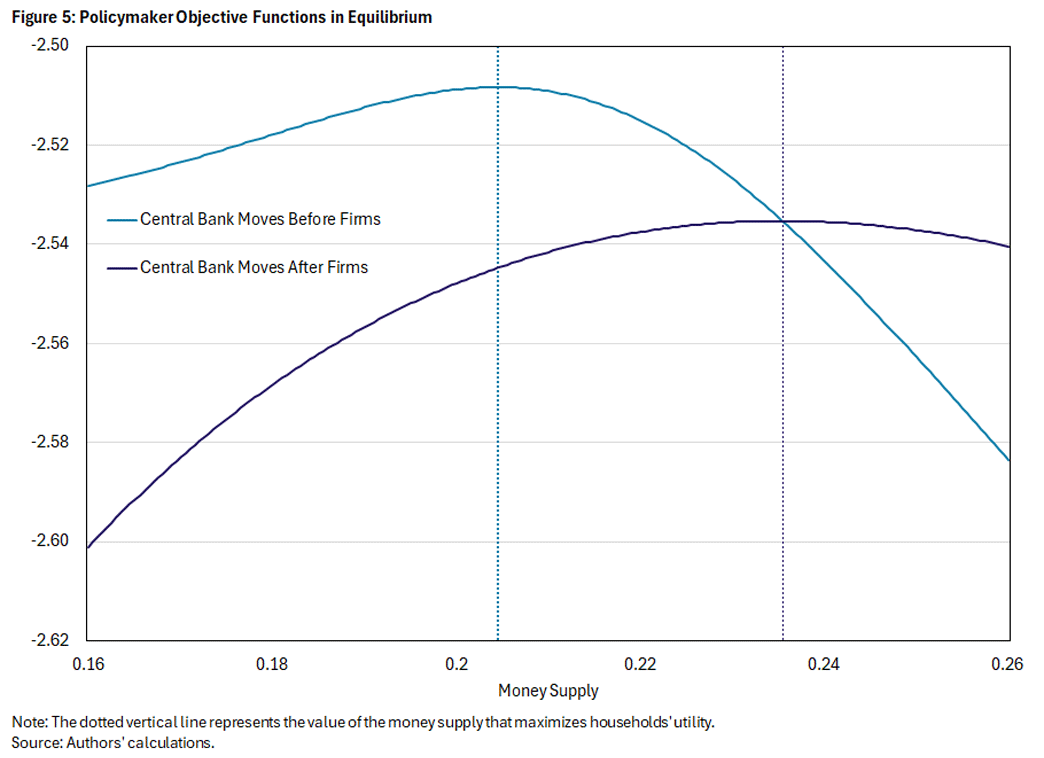
Figure 5 compares the central bank's objective functions under the two timing assumptions, with the vertical lines indicating the utility-maximizing level of the money supply. When the central bank chooses first (under VW), it faces a trade-off between reducing the markup and increasing the relative price distortion, and the trade-off is resolved with a money supply of around 0.205. When firms choose first (under AHRY), there is no trade-off for the central bank, and it eliminates the markup with a higher money supply of around 0.235. Consequently, the equilibrium inflation rate is lower when the central bank acts before firms than when firms act first.

There are other interesting aspects of Figure 5 as well. Note that the equilibrium level of utility is higher when the central bank chooses first. In the static model, the central bank choosing first can be seen as reflecting commitment: No matter what prices firms choose, the central bank is committed to a particular value of the money supply. In contrast, when firms choose first, the central bank will always adjust the money supply in response to the price. That adjustment will eliminate the markup. All else equal, eliminating the markup is beneficial, but it requires a high level of the money supply, raising inflation and the relative price distortion. When the central bank moves first, it would be feasible to eliminate the markup (Figure 2), and Figure 5 shows that this indeed would exactly reproduce the equilibrium under AHRY timing, as the objective functions intersect at this point. But it is not optimal for the VW central bank to eliminate the markup because of the larger relative price distortion that would be incurred.

Discussion

The timing of actions can be important for the qualitative and quantitative properties of equilibrium when a central bank cannot commit to its future behavior. We studied an extremely simple version of the model in VW and AHRY to gain some insight into the different quantitative results from their timing assumptions. In the fully dynamic model, other issues arise:

• Firms care about the future as well as the present.
• Under VW timing, the central bank cares about the future, because its policy decisions can influence the future, as the relative price distortion evolves slowly. (The central bank has no ability to influence the future in AHRY.)

Nonetheless, the feature highlighted here seems to be central to the difference between VW and AHRY: If the central bank cannot affect the relative price distortion, it will choose a higher money supply in equilibrium, and the inflation rate will be higher.

A natural question is: What is the "right" timing assumption? In a dynamic model, one might think that the timing would not be important, since firms set their prices for multiple periods, and there is an ongoing back and forth between the actions of firms and the central bank. That reasoning is flawed, because it ignores the importance of a "model period" in which quantities are determined. Quantities depend on the actions of firms and the central bank. Regardless of whether the model has one period or multiple periods, the intraperiod timing will determine whether the central bank can directly determine quantities or not, and this has important implications for equilibrium.

Willem Van Zandweghe is a vice president in the Research Department at the Federal Reserve Bank of Cleveland. Alexander L. Wolman is an economist and the vice president for monetary and macroeconomic research in the Research Department at the Federal Reserve Bank of Richmond. The authors thank Vinh Phan for helpful comments and excellent research assistance.

To cite this Economic Brief, please use the following format: Van Zandweghe, Willem; and Wolman, Alexander L. (October 2025) "Inflation and the Timing of Actions With Discretionary Monetary Policy." Federal Reserve Bank of Richmond Economic Brief, No. 25-40.

This article may be photocopied or reprinted in its entirety. Please credit the authors, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.

Views expressed in this article are those of the authors and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.