Have Yield Curve Inversions Become More Likely?
The recent flattening of the yield curve has raised concerns that a recession is around the corner. Such concerns stem partly from the fact that yield curve inversions have preceded each of the past seven recessions. However, other factors affect the yield curve's shape besides the expected future health of the economy. In particular, a low term premium — as has been observed in recent years — makes yield curve inversions more likely even if the risk of recession has not increased at all.
Recent changes in the yield curve have raised questions about whether a recession is likely in the near term.
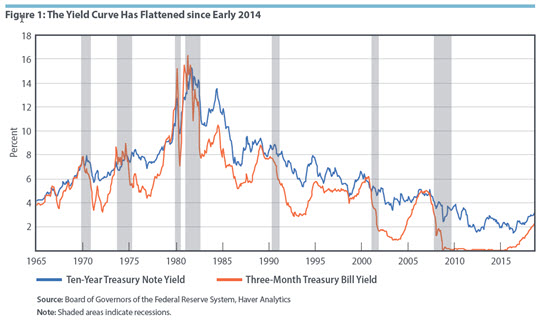
The yield curve is a graph depicting yields on U.S. Treasury bonds at multiple maturities. One can visualize yield curve behavior over time by plotting shorter-term Treasuries and longer-term Treasuries, as shown in Figure 1. When the two series move closer together, the yield curve becomes flatter. Figure 1 shows that the yield curve's slope has been declining since early 2014.
As the yield curve has flattened in recent months, questions have intensified about its predictive power. An inverted yield curve, or a situation in which long-term rates are lower than short-term rates, may suggest that markets expect a recession and thus lower interest rates in the future. Indeed, an inverted yield curve has preceded each of the past seven recessions (also shown in Figure 1).
At the same time, other things influence the yield curve besides the future strength of the economy. The Federal Open Market Committee (FOMC) acknowledged this in the minutes from its September meeting:
"A few participants offered perspectives on the term structure of interest rates and what a potential inversion of the yield curve might signal about economic prospects in light of the historical regularity that an inverted yield curve has often preceded the onset of recessions in the United States. On the one hand, an inverted yield curve could indicate an increased risk of recession; on the other hand, the low level of term premiums in recent years — reflecting, in part, central bank asset purchases — could temper the reliability of the slope of the yield curve as an indicator of future economic activity."1
This Economic Brief features Richmond Fed research assessing how one of these factors, the term premium, may affect the frequency of yield curve inversions. The term premium refers to the extra compensation investors demand (in terms of higher interest rates) to hold longer-term assets rather than shorter-term assets. If the term premium is negative, it represents what investors are willing to pay in order to lock in a long-term return. The analysis below argues that if the term premium stays as low as it has been recently — indeed, popular measures suggest it has been negative — then yield curve inversions will become more frequent even if the risk of recession has not increased at all.
What Determines the Yield Curve's Shape?
To understand the recent attention focused on the yield curve, it helps to break down its shape. The interest rate offered on a long-term Treasury bond has two components. The first component is the average of the short-term rates that are expected to prevail over the life of the bond. Expected monetary policy, and thus the health of the economy, will influence this component heavily. For example, if a recession is expected, investors may expect lower short-term interest rates in the future, which all else equal would reduce the slope of the yield curve.
The second component is the term premium. As noted, this is the compensation investors demand to hold longer-term bonds. The term premium cannot be directly measured; it is a residual, the difference between the long-term rate and the average of expected future short-term rates.
It is important to note that the first component — average expected short-term rates — makes the yield curve flat on average. At any given time, of course, the yield curve can slope upward or downward as the current short rate moves around relative to expected future short rates. But on average, expected future short rates will be neither greater nor less than the current short rate. An intuitive way to think about this is that in the absence of major structural changes to the economy, interest rates would be expected to fluctuate around a longer-term average.
Given the previous point, the fact that the yield curve usually has had an upward slope suggests the term premium has been positive on average. This does not mean the term premium is negative whenever the yield slopes down — since, as just noted, the current short rate could be higher in any given moment than expected future short rates.
To summarize, the yield curve's slope is determined by (1) the difference between average expected future short rates and today's short rate and (2) the term premium. This brings two useful insights. First, a yield curve inversion can stem from a combination of short-term rates being higher than expected future short rates (as could be the case if a recession is anticipated) and a negative term premium.
Second, if the term premium is large and positive, yield curve inversions will be rare. This has indeed been the case. A leading method for estimating the term premium, developed at the New York Fed by economists Tobias Adrian, Richard Crump, and Emanuel Moench (ACM), suggests it has averaged 1.6 percent between 1961 and today.2 And the yield curve (as measured by the difference between the three-month and ten-year Treasury yields) has been inverted 10 percent of the time since 1961.
How Likely Is Inversion as the Term Premium Falls?
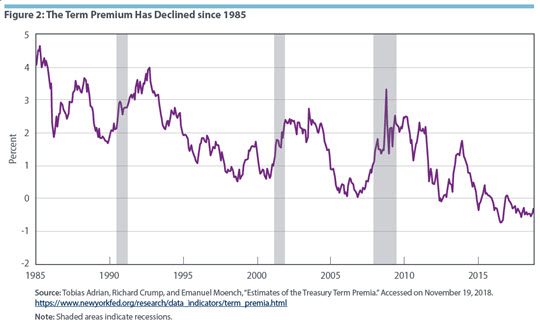
The flip side of the previous point is that if the term premium narrows, yield curve inversions will become more likely even if there is no increased risk of recession. And, indeed, there is reason to believe the term premium has fallen. Recently, the ACM model's estimates of the term premium have moved persistently lower. The average values since 2006 and 2012 are 0.77 and 0.20, respectively. (See Figure 2).3
Two authors of this Economic Brief (Wissuchek and Wolman) recently evaluated how changes in the term premium affect the likely frequency of yield curve inversions.4 In principle, one could do this by conducting a statistical analysis of historical data to assess the relationship between the level of the term premium and the frequency of yield curve inversions. However, the number of inversions is too small to produce a reliable estimate using this method. Instead, Wissuchek and Wolman's exercise involved simulating data for the short-term interest rate and then measuring how the frequency of yield curve inversions in the simulated data varies with the behavior of the term premium.
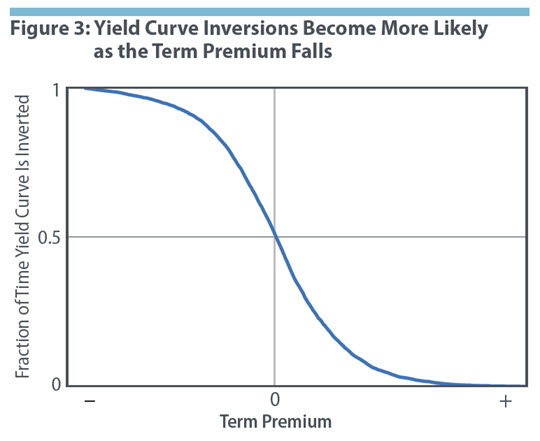
To build intuition for this simulation exercise, Figure 3 illustrates the qualitative relationship that would arise between the frequency of yield curve inversions and the level of the term premium if the term premium were fixed at different levels. For very high values of the term premium, the yield curve would never be inverted because the expected decrease in short-term rates would never be large enough to outweigh the term premium. Conversely, for very low (negative) values of the term premium, the yield curve would always be inverted because the expected increase in short-term rates would never be large enough to outweigh the term premium. And, if the term premium were fixed at zero, then over long periods the yield curve would be inverted roughly half the time. In reality, the term premium is not constant, so the simulation involves looking at how the frequency of yield curve inversion varies as the distribution of the term premium changes.
Simulating data for the yield curve slope requires making assumptions about the behavior of the short-term interest rate and how expectations of future short-term interest rates are determined. With these assumptions, one can then simulate a long sample of data for the short-term rate and determine the expectations portion (the first component) of the slope of the yield curve in each period of that long sample. Repeating this process for different distributions of the term premium then allows one to trace out the relationship between the frequency of inversion and the term premium.
Naturally, the relationship traced out is only as reliable as the assumptions about short-term interest rates. Wissuchek and Wolman's assumptions are as follows: first, they assume the behavior of real short-term interest rates from 1985 to the present is a good model for the behavior of real short-term interest rates generally. Arguably, this behavior represents "optimal" monetary policy since monetary policy was not an obvious source of instability in the economy during this period. Second, they assume that expected inflation is constant at 2 percent, which implies that all fluctuations in the short-term nominal rate stem from fluctuations in the short-term real rate. Together, these assumptions provide a model for the short-term nominal rate that allows one to simulate data for the short-term nominal rate.
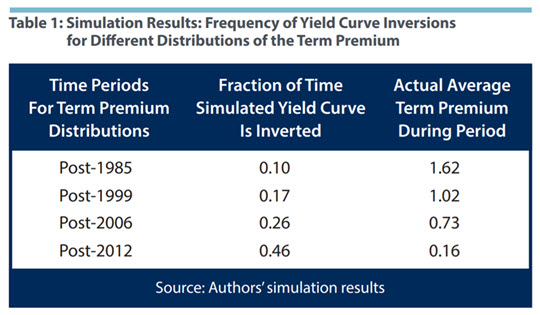
The next step is to generate expectations of future short-term interest rates. Wissuchek and Wolman assume that expectation formation is consistent with the process that generates the simulated short-term rates, an assumption known as rational expectations. With simulated data on short-term rates and expected future short-term rates, they compute the expectations portion of the slope of the yield curve. The actual slope of the yield curve also depends on the term premium: Table 1 shows how the frequency of yield curve inversion in these simulations would vary with the distribution of the term premium.
Figure 2 shows that the term premium has generally been declining over the past thirty years, so the logic of Figure 3 suggests that yield curve inversions ought to become more likely. Indeed, the simulations suggest that if term premia are drawn from their post-1985 distribution, the yield curve would be inverted 10 percent of the time, whereas if term premia are drawn from their post-2012 distribution, the yield curve would be inverted 46 percent of the time.
Conclusion
If the term premium is persistently high, as it was throughout the 1980s and early 1990s, then the average slope of the yield curve will be positive and large. But estimates of the term premium have trended down since the mid-1980s, and over the past six years, the term premium has fluctuated around an average value near zero. This Economic Brief has argued that if the term premium continues in that range for the foreseeable future, then yield curve inversions will be much more likely in the future, all else (such as the state of the economy) equal.
An important caveat is that this analysis treats the term premium as exogenous, which it clearly is not. For example, perceptions about monetary policy can influence the term premium: if investors are concerned about long-run instability of inflation, this may raise the return required on long-term bonds. And, as noted at the outset, factors that may have been in play recently include central bank asset purchases. It is useful to think of the above analysis as an exercise that asks: How would a declining term premium influence the shape of the yield curve holding other factors constant?
The message is simple: if the term premium stays persistently low or negative, then yield curve inversions are likely to become more frequent even if recessions have not become any more likely.
Renee Haltom is manager of editorial content, Elaine Wissuchek is a research associate, and Alexander L. Wolman is a vice president in the Research Department of the Federal Reserve Bank of Richmond.
See Tobias Adrian, Richard Crump, and Emanuel Moench, "Treasury Term Premia Estimates," Federal Reserve Bank of New York. Accessed on November 19, 2018.
The term premium is influenced by factors that are not directly measurable, so it is difficult to say precisely why estimates of the term premium have declined. However, some research suggests that a decline in inflation risk has been a contributing factor. See Michael D. Bauer, "A New Conundrum in the Bond Market?" Federal Reserve Bank of San Francisco Economic Letter No. 2017-34, November 20, 2017; and Eric Swanson, "What We Do and Don't Know about the Term Premium," Federal Reserve Bank of San Francisco Economic Letter No. 2007-21, July 20, 2007.
Analysis from a forthcoming article in the Federal Reserve Bank of Richmond Economic Quarterly.
This article may be photocopied or reprinted in its entirety. Please credit the authors, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.
Views expressed in this article are those of the authors and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.
Receive a notification when Economic Brief is posted online.