COVID-19 over Time and across States: Predictions from a Statistical Model
We discuss a statistical time series model to capture and forecast the dynamics of COVID-19 in the fifty U.S. states and Washington, D.C. We design the model to replicate the typical pattern of infections during a pandemic. We rely on Bayesian methods, which provide a straightforward way to quantify the uncertainty surrounding our estimates and forecasts. In this brief, we focus on North Carolina and Washington, D.C., since they have experienced different trajectories of COVID-19 and may have different implications for the efficacy of our approach.
The COVID-19 pandemic has presented challenges for forecasting and policy design. We confront these issues using a statistical time series model — developed in Ho, Lubik, and Matthes (2020) — that captures the dynamics of the COVID-19 pandemic in the fifty U.S. states and Washington D.C.1 In this brief, we focus on North Carolina and Washington, D.C., as illustrative examples.
To model the dynamics of COVID-19, we first note that the time path of infections during a pandemic follows a typical pattern. When a pathogen enters a population that is susceptible to infection, the number of cases is low initially. However, the growth rate of new infections is high and tends to be exponential because each infected person creates a chain of new infections. But at some point, the pathogen runs out of susceptible hosts because they are already infected, immune, or simply not physically present because of health policies such as social distancing. At this inflection point, the growth rate decreases until it eventually hits zero.
We replicate this broad pattern by specifying a flexible functional form that describes the path of infections over time. In addition, we allow the number of deaths to depend flexibly on the daily number of new cases up to thirty-five days prior. In contrast to theoretical epidemiological models, our empirical specifications have more leeway to follow the data and are not constrained by precise theoretical relationships that may be specified incorrectly. The model is able to fit the path of the pandemic in the fifty U.S. states and D.C., producing forecasts that perform well.
In addition, our modeling approach explicitly reflects the uncertainty of this model's estimates and the uncertainty inherent in forecasting the trajectory of a virus. The precision of a forecast — or how tightly other possible forecast paths are concentrated around the most plausible path — is generally affected by two factors: first, the uncertainty of the model's estimates in terms of overall fit and parameter estimates; and second, the extent to which the model may be subject to further disturbances or imprecise data collection in the future. We take both factors into account to give a sense of how uncertain forecasts in a pandemic truly are.
We extend the model in a panel dimension and introduce time variation in the parameters. The panel dimension captures and uses the differences across U.S. states because the dramatic contrast in outcomes between, for instance, New York and California makes it clear that understanding differences, even within one country, is an important component in addressing the public-health challenge. In addition, we allow the parameters in our model to depend on time-varying, state-level measures of social distancing and testing, providing an estimate of the relationship between these variables and the trajectory of cases.
The Evolution of Forecasts over Time
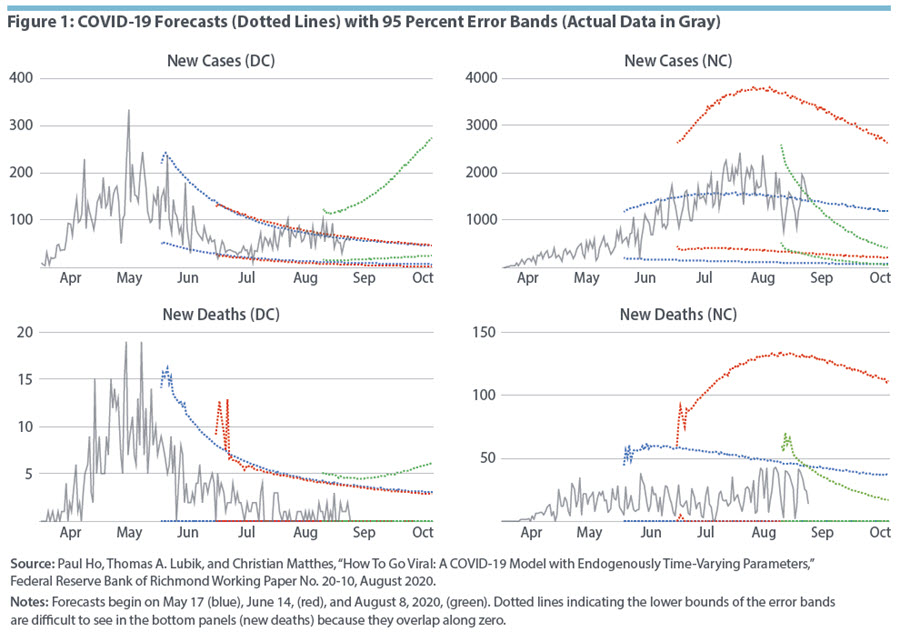
As the COVID-19 pandemic unfolds across the United States, not only do the model's predictions update to reflect the new data, but the uncertainty around those predictions also changes. We illustrate this evolution for Washington, D.C., and North Carolina in Figure 1, where we show 95 percent forecast error bands for forecasts taken from May 17, June 14, and August 8, 2020. The bands for the three forecasts are denoted by the blue, red, and green lines, respectively. A wider gap between lines of the same color indicates greater uncertainty for that forecast.
Although the forecasts are largely borne out by the data, we find substantial updates in the forecast levels and variances. In D.C., the forecasts are almost identical when taken from May 17 and June 14. However, by August 8, not only is the forecast revised upward, but the error bands become substantially wider. With the second peak in cases at the end of July, uncertainty about the model's parameters increased, as it was unclear whether the spike in daily cases was a temporary deviation from the previously predicted decline or a fundamental change in the long-run trend. Even if the increase was only temporary, it indicated the possibility of large disturbances that could lead to greater volatility in the future path of the pandemic. In North Carolina, the forecasts are revised upward and become more uncertain between May 17 and June 14 but tighten significantly by August 8, especially at longer horizons. The sharp increase in cases between May 17 and June 14 plays a similar role to the D.C. data in the second half of July, causing increased forecast variance from both parameter uncertainty and shock volatility. However, by August 8, North Carolina had experienced a distinct peak in cases, and error bands narrowed to reflect tighter parameter estimates.
The Effects of Policy Measures on Time Variation in the Parameters
Our panel model allows for a specific form of time variation in the parameters in that we assume they depend on observed factors. To choose these predictors, we assess how likely and important they are in affecting the time path of a pandemic. We focus on two variables. First, we allow the path of infections to depend on the Mobility and Engagement Index (MEI), which measures the degree of social distancing in terms of a broad index of travel.2 The MEI is derived from geolocation data from millions of mobile phones, which show density and frequency of travel activity and its direction. For instance, these data would reflect the number of trips taken to the local mall. Next, we allow both the path of infections and the mortality rate to depend on the positive test rate, defined as the ratio of reported cases to number of tests performed, which indicates the intensity of testing in each state. (A lower positive test rate generally indicates more extensive testing.) While neither of these metrics is strictly controlled by government or health authorities, they can be influenced by policy to some extent. For instance, the degree of social distancing can be mandated by lockdowns or travel restrictions, and it also can be driven by personal decisions. Similarly, the availability of testing kits can be supported financially and logistically by local and federal authorities, but it also depends on investment from the private sector.
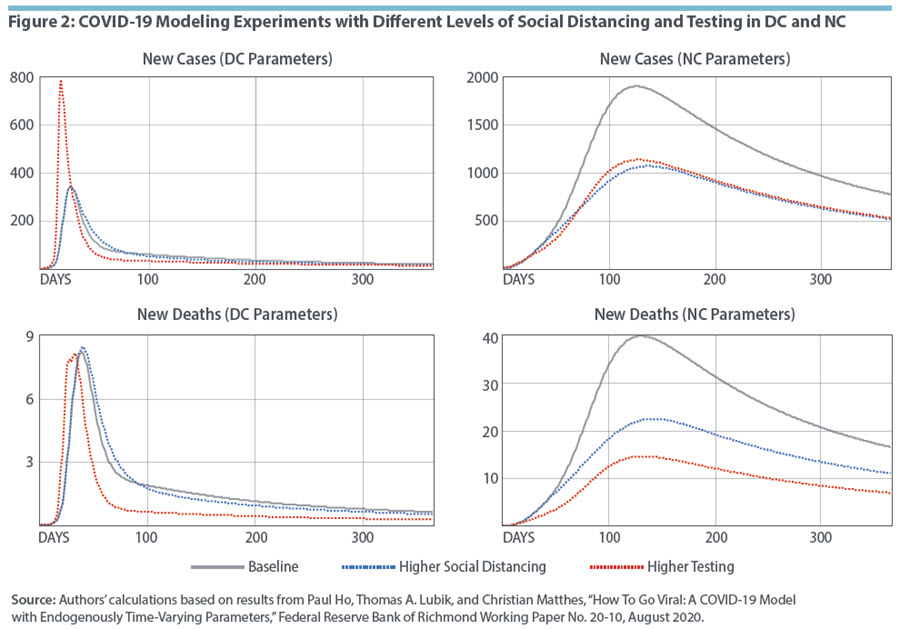
We conduct the following experiments, which are depicted in Figure 2. Using North Carolina and Washington, D.C., as examples, we plot the model-implied paths of cases and deaths in the absence of disturbances under the median estimates for the two states. We compare these trajectories to those associated with different possible paths for the MEI and positive test rate in both North Carolina and Washington, D.C. The paths for the MEI and the testing variables are chosen to reflect the underlying data.
Under this baseline calibration (shown in gray), the pandemic in D.C. (top left panel) led to a quick increase in new cases reaching a peak of around 350 per day about one month after the initial cases were reported. The number of new cases declined quickly beyond that peak but then declined only slowly to the point where 150 days into the pandemic, it cannot be considered over. North Carolina is naturally different in terms of the number of cases (top right panel), but the pattern of infections is similar, albeit much more drawn out. North Carolina reaches a peak of new infections about 120 days after the first reported cases, with an even slower decline after the peak. In terms of deaths (bottom panels), the timelines and patterns are similar since the model implies that deaths follow infections with a lag. Qualitatively, the baseline trajectories match the empirical path of infections and deaths reported in both D.C. and North Carolina.
We first consider the experiment of a time path for the MEI that implies a high level of social distancing. This could be government-imposed or self-directed as risk awareness grows in the population. While the baseline path of the MEI was chosen to be similar to the actual path in North Carolina, the alternative with a high level of social distancing more closely resembles the path that was followed by D.C. The implied time paths for deaths and infections in the two localities are shown as dotted blue lines. In the case of Washington, D.C., the implied outcome under more social distancing almost exactly coincides with the baseline estimation. This suggests that, given the specific conditions in the nation's capital, the higher level of social distancing did not lead to a substantially lower number of cases. In contrast, for North Carolina, more social distancing would have led to cutting the number of infections and more importantly the number of deaths in half. While other considerations may have come into play, such as the structure of the economy in Washington, D.C., where a larger fraction of the population might have been able to work from home, our counterfactual analysis suggests alternative policy paths could have reduced the spread of the virus in North Carolina.
We also consider how the model-implied path changes when the positive test rate is decreased from 10 percent to 5 percent. In Figure 2, the paths corresponding to the 5 percent positive test rate, which is associated with more testing than the baseline, are denoted by the red dotted lines. In D.C., we find that more extensive testing is associated with a larger number of reported cases, with a peak of approximately 800 new cases per day instead of 350 (top left panel). However, the peak for the model-implied path for new deaths (bottom left panel) remains unchanged, suggesting that the increase in reported cases comes primarily from improved detection rather than an actual increase in COVID-19 infections. A lower positive test rate typically corresponds to more asymptomatic or mildly symptomatic patients being tested, leading to a lower number of deaths per reported cases since a larger pool of tested individuals tends to include more lower-risk people. These results emphasize that the interpretation of reported case numbers depends on the level of testing in a locality. For North Carolina, our model associates the increase in testing with a reduction in cases by slightly less than half and a reduction in deaths by about two-thirds. These results suggest that greater testing in North Carolina could have decreased the number of infections by, for instance, enabling infected individuals to quarantine earlier and avoid spreading the virus.
A key observation from our numerical experiments is that the effect of policies can vary across localities. Countries, states, and cities differ along many dimensions, including demographics, industry composition, and population density. These factors not only influence the spread of the virus but can also affect the outcome of policy interventions, such as lockdowns or increased testing. Furthermore, local conditions also impact the spillover of public-health policy into the economy.
Our analysis can only be suggestive. It is subject to the criticism that the behavior of a reduced-form relationship changes when underlying policy variables, in our case, the MEI and positive test rates, change, so that inference about future outcomes is unreliable. More specifically, a high number of cases likely leads to more stringent social distancing measures, so that the MEI cannot be considered exogenous. Therefore, statements to the effect that social distancing causes the number of cases to change are imprecise in that they likely underestimate the effect. Nevertheless, we would advocate for counterfactual analysis like this as a tool to understand how the dynamics of a virus's spread change with policy-relevant measures.
Conclusion
In this brief, we highlight a statistical model of the COVID-19 pandemic in the United States. We built the model around insights from epidemiological research into how pandemics evolve over time, but the model also allows for flexibility in how patterns of infections and deaths are described in aggregate and state-level data. The model is able to fit the time path of the pandemic across the fifty U.S. states and Washington D.C., while providing transparent quantification of forecast uncertainty. In addition, the model allows for a form of time variation in its parameters in that they depend on variables that likely influence the shape and time path of the pandemic. The time variation allows us to perform counterfactual policy analysis, to some extent, by positing alternative paths of exogenous, perhaps policy-driven, factors and tracing out their impact on the forecast.
There is a tradeoff between the parsimony and transparency of our statistical model with the detail of more sophisticated models. For example, our model's predictions are predicated on assumed paths for social distancing and testing. These are not perfectly controlled by policy. Their future paths are uncertain and can also be influenced by the path of the pandemic. In addition, we have omitted numerous other variables, such as demographics and industry composition, that may further influence the outcomes of the pandemic. Despite these simplifications, our model captures the striking and complex ways that new data and the specifics of a locality can influence the predicted path of the virus and its response to policy.
Paul Ho is an economist and Thomas A. Lubik is a senior advisor in the Research Department at the Federal Reserve Bank of Richmond. Christian Matthes is an associate professor of economics at Indiana University.
For a more detailed description of the model and results for each state and Washington, D.C., see Paul Ho, Thomas A. Lubik, and Christian Matthes, "How To Go Viral: A COVID-19 Model with Endogenously Time-Varying Parameters," Federal Reserve Bank of Richmond Working Paper No. 20-10, August 2020.
The Federal Reserve Bank of Dallas produces the Mobility and Engagement Index, which summarizes information from seven different variables based on geolocation data collected from mobile devices to gain insight into the economic impact of the pandemic. The MEI measures the deviation from normal mobility behavior induced by COVID-19.
This article may be photocopied or reprinted in its entirety. Please credit the authors, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.
Views expressed in this article are those of the authors and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.
Receive a notification when Economic Brief is posted online.