Innovation, Diffusion and Intellectual Property Rights

Our recent working paper studies innovation and diffusion of technology along an industry's evolution and characterizes how diffusion affects the incentives to innovate. In our analysis, firms participate in a competitive industry and face production capacity constraints. The entry of imitators thus increases industry supply and is socially beneficial to a degree. We show that, from the social welfare point of view, innovators should be compensated for intellectual property rights to internalize their knowledge spillovers to imitators. However, such compensation should be only partial due to the congestion externality in the meetings between innovators and imitators where idea diffusion takes place.

Innovation and diffusion are fundamental drivers of technological progress and long-run growth. An innovation cannot fulfill its potential without being widely adopted, but rapid diffusion and imitation may reduce the incentive to innovate due to innovators missing out on potential compensation. In my recent working paper "Idea Diffusion and Property Rights" — co-authored with Boyan Jovanovic — we study the interplay between innovation and diffusion in a competitive industry setting and explore the welfare and policy implications.

Background

The paper is motivated by several salient facts. For one, as an industry evolves from birth to maturity, the number of firms typically grows following a S-shaped curve. A large theoretical and empirical literature has explained such a growth pattern as a technology diffusion process.¹ Specifically, ideas diffuse through random meetings between existing and potential adopters of a new technology, giving rise to a S-shaped diffusion curve. (A similar process also has been used by researchers to explain the spread of contagious diseases such as COVID.)

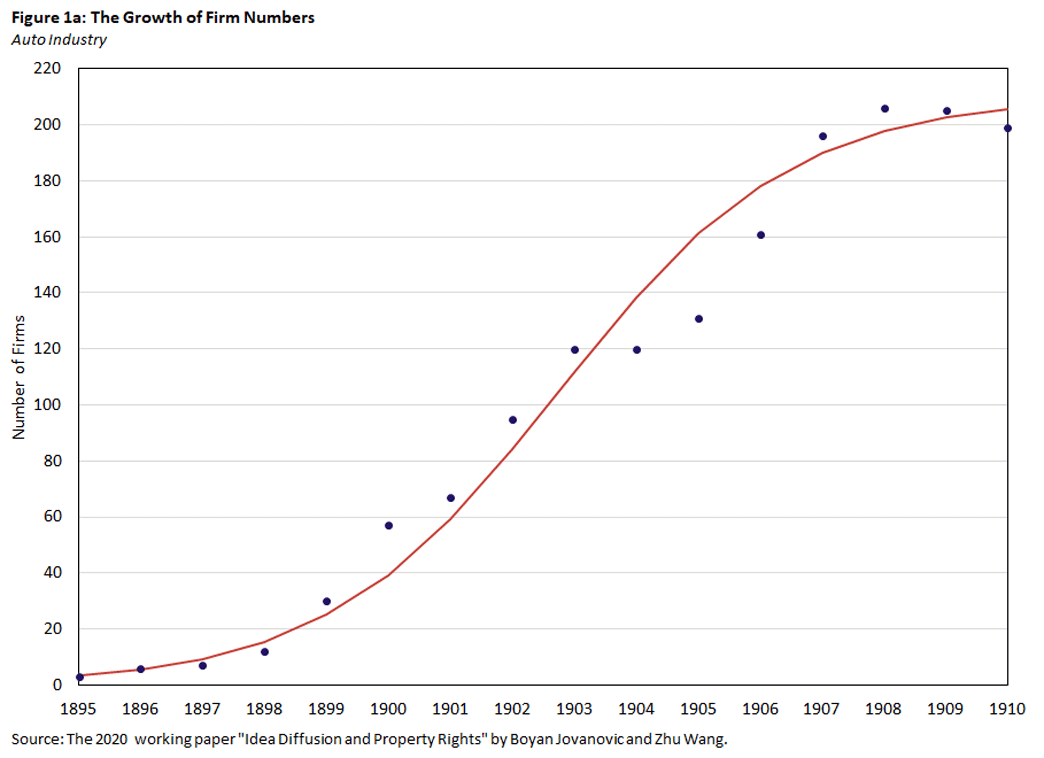
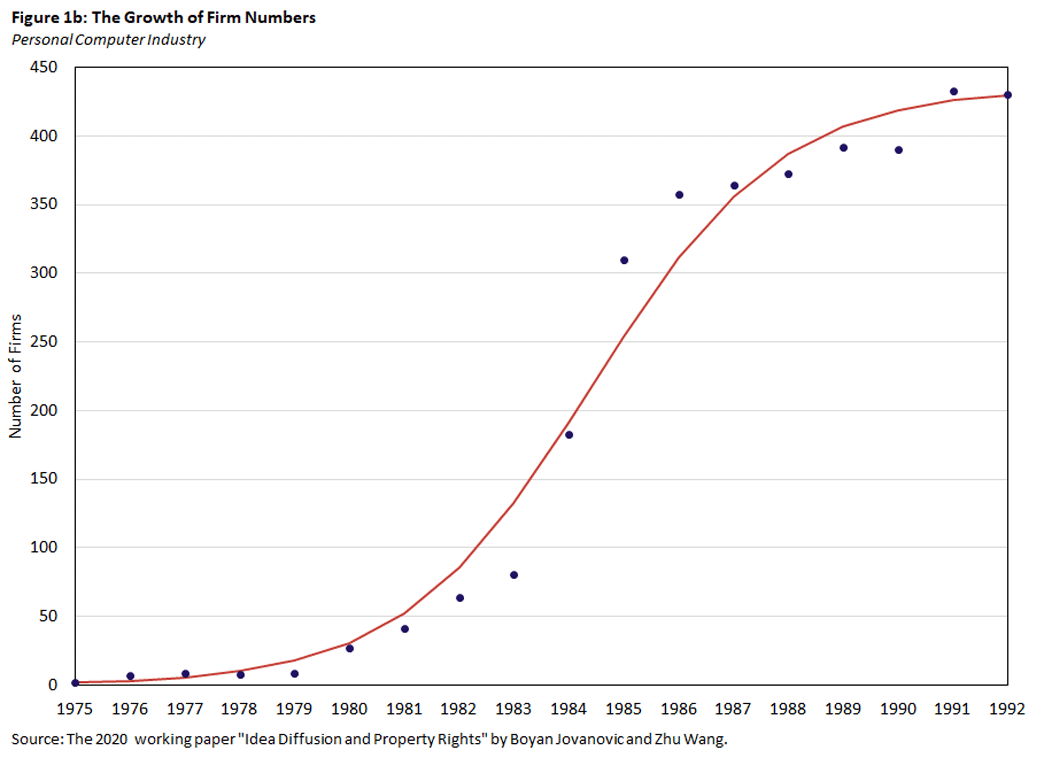
Figure 1 plots the time path of firm numbers in the U.S. automobile industry and personal computer industry. In each industry, the number of firms grows along a S-shaped curve.

Mathematically, one can assume agents that have adopted a new technology meet future potential adopters via a quadratic matching function to spread the innovation. As shown by the figure, such a meeting process gives rise to a logistic diffusion curve (so that the percentage of adopters follows a logistic distribution over time), and the estimated curve matches the data of firm numbers very well.²

Given the diffusion process, innovators enjoy substantial rents during the early stages of industry evolution, which provide incentives to innovate even in competitive industries. This is in contrast with the conventional wisdom that monopoly is a necessary condition for innovation. According to the conventional view, a competitive market would drive price to marginal cost of production. As a result, innovators would not be compensated for their investment on innovation and thus would have no incentive to innovate.

However, recent studies — such as the 2008 paper "Perfectly Competitive Innovation" — provide ample evidence that competitive innovations are pervasive in modern day marketplaces and in history. The conventional argument overlooks the fact that it takes time for a new industry to build production capacity.

When a new product comes to the market, only a few firms know how to produce it before the innovation gets widely diffused and imitated, and each firm faces production capacity constraints. Therefore, for an extended period, there is only a limited supply of the new product, and the price stays well above the marginal cost. This creates competitive rents to the innovators and provides incentives for innovation.

Against this backdrop, several important questions arise. How do innovation and diffusion interplay and drive the evolution of a competitive industry? How do diffusion and imitation dissipate innovators' rents? What is the socially optimal way to compensate innovators?

Theoretical Analysis

To answer these questions, we construct a dynamic model of industry evolution and study the impact of diffusion on the incentives to innovate. The model considers a competitive industry with a downward sloping demand curve for a homogeneous good and a group of potential producers.

An innovation or "idea" enables an agent to produce the good subject to a capacity constraint. At the outset, agents decide whether to pay a sunk cost to innovate. Some will do so immediately, while others may consider innovating later or wait to imitate the innovation.

Imitation occurs in random pairwise meetings between those who have the idea and those who do not. Imitation is costless, but the imitator may have to pay a fee to the idea seller, and the fee is determined by the latter's bargaining share. We study two regimes regarding the payment for ideas:

• In Regime 1, imitators cannot resell ideas to other imitators. A potential adopter can copy an idea from an imitator, but the fee goes to the idea's original innovator and not to the imitator. (This scenario is typically seen in franchising or patents with compulsory licensing.)
• In Regime 2, imitators can resell ideas to other imitators and keep the proceeds, a scenario which is often relevant for non-patented know-how or patents that allow sublicensing.

Our theory yields the following findings. First, under each regime, the value of entering as an innovator declines over time due to the falling revenues from selling the good and the idea. As a result, innovators enter the industry only at the beginning, and the number of imitators then follows an S-shaped logistic diffusion curve. We show that more innovators enter in Regime 1 or when idea sellers' bargaining share is larger, which results in faster industry growth.

Second, the socially optimal compensation for innovators should be only partial. On one hand, innovators generate knowledge spillovers to imitators, so some compensation is needed for innovators to internalize this positive externality. On the other hand, innovators also create a meeting congestion externality: An agent's decision of entering as an innovator instead of an imitator reduces the chance for other innovators to meet imitators to sell ideas. Therefore, from the social welfare viewpoint, innovators should be compensated, but not fully. Moreover, we find that the socially optimal compensation of idea sellers (in terms of their bargaining share) should be larger in Regime 2 where innovators collect the payoff of ideas partly indirectly.

Third, a policy that restricts the speed of diffusion reduces welfare. Our analysis finds that such a policy encourages entry of innovators and raises initial industry capacity, but it lowers imitation and leads to slower growth of capacity. Applying the analysis to non-compete contracts (which restrict labor mobility and thus idea diffusion), our finding suggests that their enforcement in Massachusetts but not in California — where a state statute bans their enforcement — may explain why venture activity on the once-dominant Route 128 tech industry corridor in Massachusetts was overtaken by that in Silicon Valley.

Empirical Applications

We apply the model to two historically important industries: automobile and personal computer. We use these industries because idea diffusion played an important role in each's development. Though they started 80 years apart, the two industries shared the basic feature of an S-shaped diffusion in their early years, as shown in Figure 1.

Using model calibration and counterfactual exercises, we evaluate and quantify our theoretical predictions. We find that the automobile and the personal computer industries both feature highly elastic demands, under which entry of imitators can drive prices down only slowly. Because this encourages innovation but exacerbates the congestion externality, the socially optimal bargaining share of idea sellers should be low for both industries, and it should be lower for the more price-elastic personal computer.

Quantitatively, our benchmark analysis finds that the socially optimal bargaining share for idea sellers is 7.0 percent in Regime 1 and 16.7 percent in Regime 2 for the automobile industry. The corresponding shares are 5.5 percent in Regime 1 and 13.5 percent in Regime 2 for the personal computer industry. Alternatively, the social optimum can, in principle, be achieved by subsidizing 61 percent of the innovation cost in the automobile industry or 62 percent in the personal computer industry.

Conclusion

We study innovation and diffusion over a competitive industry's evolution. Our analysis shows that, with capacity constraints, licensing raises the revenues of innovators and is also socially beneficial to a degree. The welfare outcome depends on whether imitators can resell the innovation and on how much the innovators are compensated for transferring the innovation.

We find that the socially optimal compensation for innovators should be only partial due to the congestion externality in meetings between innovators and imitators. This agrees with findings in some recent papers on aggregate growth. For example, the 2020 working paper "Knowledge Creation and Diffusion With Limited Appropriation (PDF)" shows that due to matching congestion, the growth-maximizing bargaining share of innovators depends on the parameters in the matching function.³ The 2021 paper "Reconciling Models of Diffusion and Innovation: A Theory of the Productivity Distribution and Technology Frontier" shows that innovators' licensing income becomes highly elastic with regard to the license price when innovators' bargaining power is too strong and that this can lower licensing income and growth.

Our analysis also suggests that with a given compensation share for innovators, slowing down diffusion encourages innovation and raises initial capacity, but that it lowers imitation so that capacity grows more slowly. We argued that this may help explain why Silicon Valley overtook Route 128.

Finally, we apply the model to the U.S. automobile industry and personal computer industry, and the empirical results match the evolution pattern of both industries well and quantify our theoretical findings.

Zhu Wang is vice president for research in financial and payments systems in the Research Department at the Federal Reserve Bank of Richmond.

To cite this Economic Brief, please use the following format: Wang, Zhu. (July 2023) "Innovation, Diffusion and Intellectual Property Rights." Federal Reserve Bank of Richmond Economic Brief, No. 23-23.

This article may be photocopied or reprinted in its entirety. Please credit the authors, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.

Views expressed in this article are those of the authors and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.