Mortgage Spreads and the Yield Curve
Mortgage spreads — the 30-year mortgage fixed rate minus the 10-year Treasury rate — have a history of increasing sharply in times of economic stress. While often viewed as a measure of financial stress, I argue they are mostly explained by changes in expected mortgage duration arising from changes in the yield curve. Economic stress leads to a downward-sloping yield curve, which increases expected refinance activity, shortening mortgage durations. This shorter duration makes mortgages prices reflect short (rather than long) Treasury rates. But with a downward-sloping yield curve, this means mortgage rates will be unusually high relative to the 10-year Treasury.
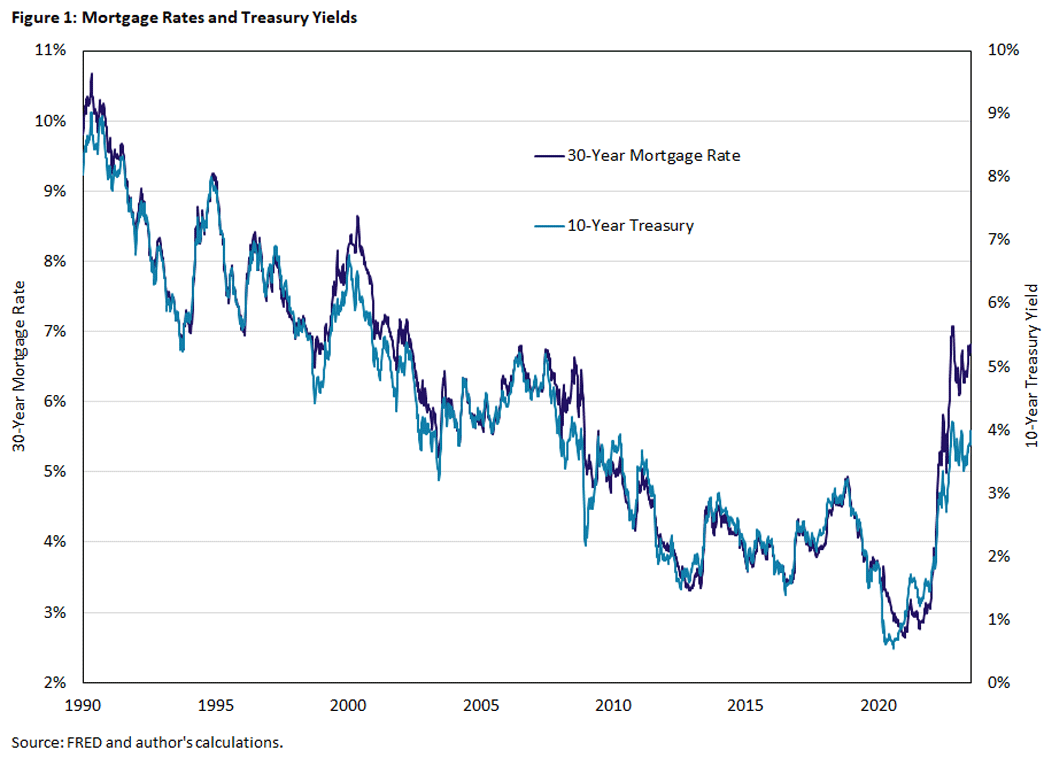
Mortgage interest rates typically follow the yield of the 10-year U.S. Treasury closely. This can be seen in Figure 1, where they have moved in tandem for more than 30 years.1
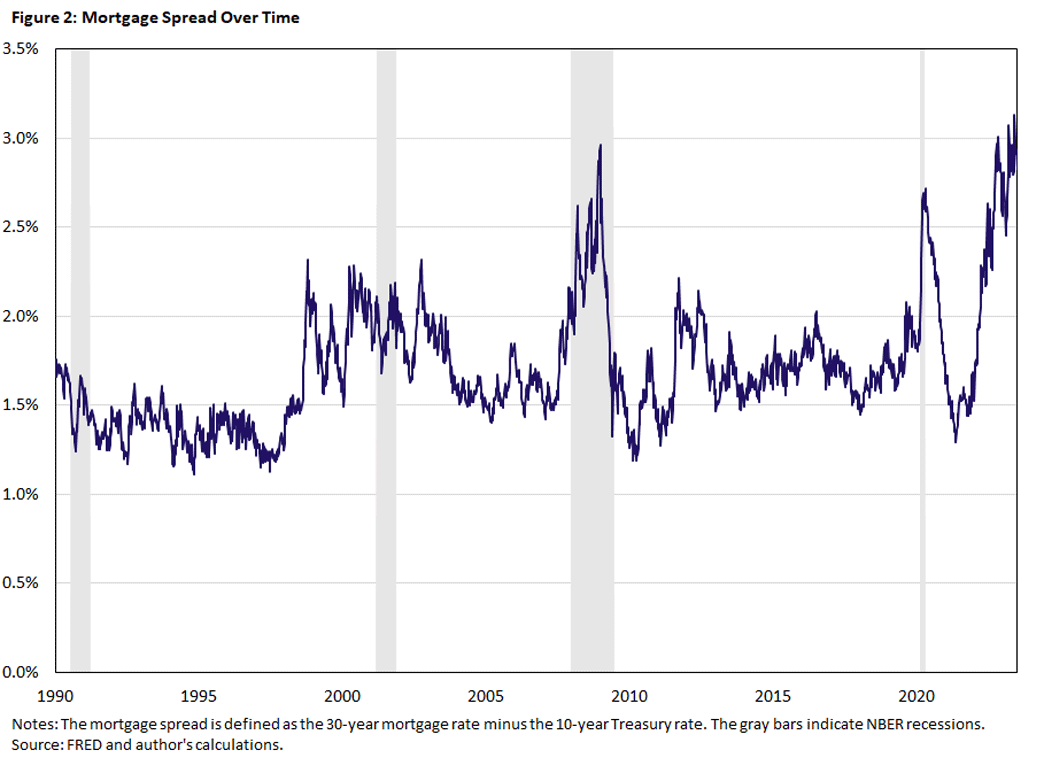
However, during periods of economic stress, the comovement breaks down. Figure 2 shows this by plotting mortgage spreads — the average rate of a 30-year fixed mortgage minus the 10-year U.S. Treasury yield — over time. The gray regions in the figure denote recessions, which is when the mortgage spread tends to blow out. However, there are some other periods (like in the late 1990s) where the spread increases sharply without a recession.
How should one interpret this dislocation? One explanation is that lending dries up in these periods as lenders become effectively more risk averse and demand higher spreads. In this article, I advocate for an alternative interpretation: The mortgage spread blows up in recessions for two reasons:
- The yield curve inverts, which shortens the expected duration of mortgages.
- Since the yield curve is inverted, short-duration assets have higher yields (all else equal) than longer-duration assets.
These two forces jointly drive up the 30-year mortgage spread relative to the 10-year Treasury (T10). I will call this interaction the mortgage duration effect.2
I will first establish empirical evidence for the mortgage duration effect of the mortgage spread. I will then show that an economic model — with fully rational agents and competitive, risk-neutral lenders — is able to reproduce the mortgage duration effect.
Empirical Evidence
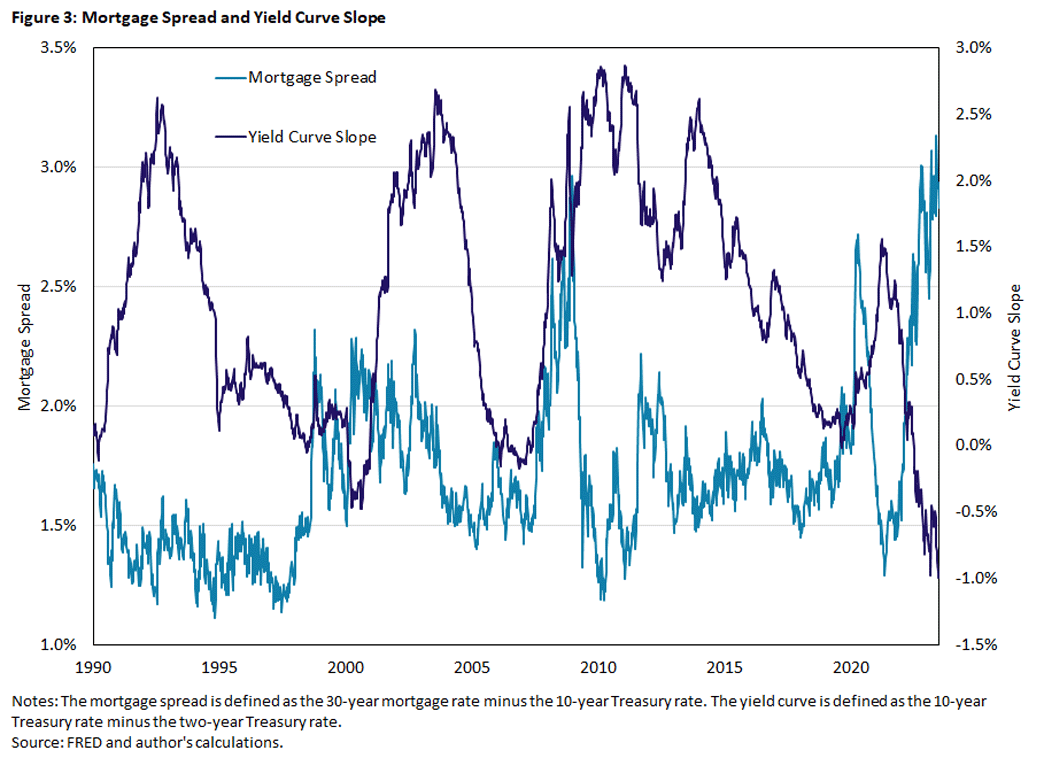
Strong empirical evidence for the mortgage duration effect comes from examining the behavior of the mortgage spread against the yield curve slope. Figure 3 plots time series for the mortgage spread and the yield curve slope, which I define here as the spread of the 10-year Treasury minus the two-year Treasury (T10T2). The connection between the two series is far from obvious, although statistically, there is some negative correlation (-0.24).
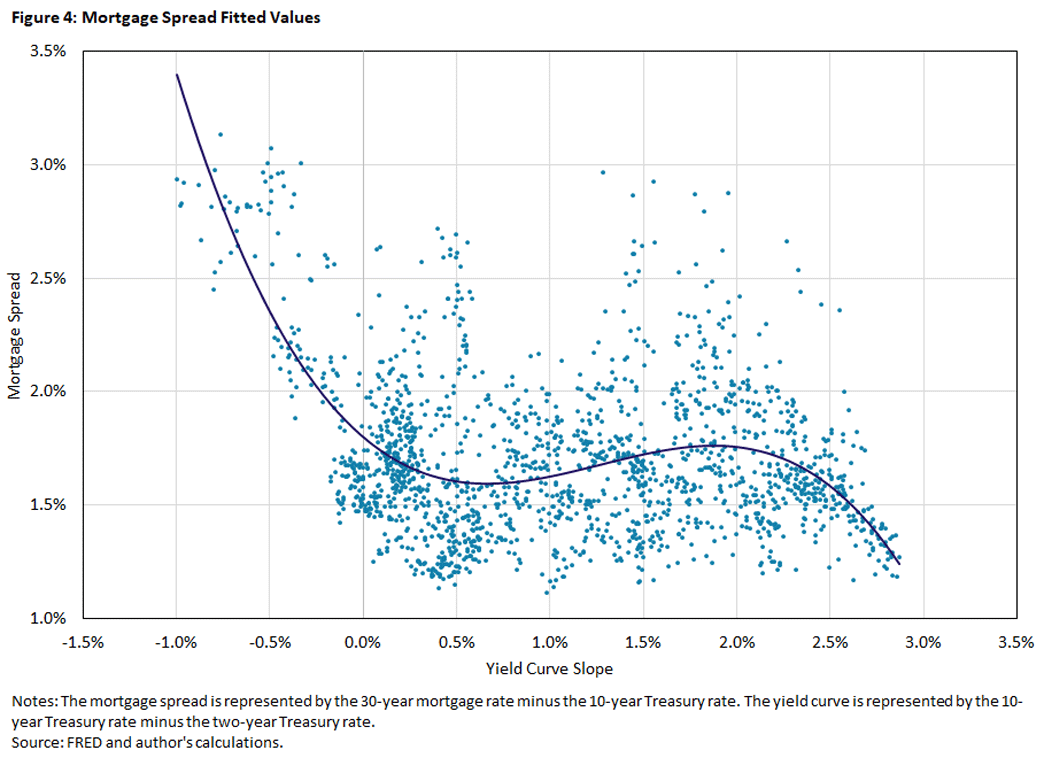
The relationship becomes much clearer when looking at a scatter plot, as Figure 4 does. The relationship is not uniform but hinges whether the T10T2 spread is above zero. When the T10T2 spread is positive — which is when the yield curve is upward sloping — there's only a slight negative relationship between T10T2 and the mortgage spread. (The correlation is -0.03.)
However, when the T10T2 spread is negative (indicating a downward sloping yield curve), the relationship becomes sharply negative, with a correlation of -0.84. Crucially, backward-bending yield curves tend to arise in recessions. Consequently, this feature lends itself to generate large increases in mortgage spreads that occur just as the economy is slipping into recession.
But why should one expect any relationship between the T10T2 spread and the mortgage spread, and why should it hinge on upward or downward sloping yield curves? Refinancing behavior is the key mechanism. When the yield curve is upward sloping, rates tend to increase over time. This means current mortgage rates are likely to be lower than future mortgage rates.
In this case, individuals and households are more likely to stay with their mortgages for extended periods, making mortgages a long-duration asset. As a long-duration asset, competition dictates that its interest rate should reflect the interest rate of other long-duration assets, like the T10.
In contrast, when the yield curve is downward sloping, rates tend to decrease over time. With current mortgage rates likely higher than future mortgage rates, individuals and households are expected to refinance quickly. This makes mortgages short-duration assets. And as a short-duration asset, their interest rates should more closely align with the two-year Treasury rate (T2) than the T10. Since the T2 is larger than the T10 in this downward sloping environment, this means the mortgage spread should be large.
Model Evidence and Description
To corroborate this empirical evidence, I test whether a model with fully rational agents and competitive, risk-neutral lenders can generate the empirical relationship between the mortgage and T10T2 spreads.
In the model, every household owns a house and chooses whether to stay with its current mortgage or refinance to a new one. Refinancing induces a refinance cost equal to 2 percent of the house value.3 Mortgages are modeled as consols (interest-only loans), but their effective durations are at most 30 years because of an additional 0.83 percent exogenous chance of refinancing per quarter. This exogenous probability both limits the average duration of mortgages and captures factors such as marriage, death, childbirth, job loss and faraway job offers that result in early mortgage termination.
Households are risk-neutral and have a discount factor of 0.99. When deciding to refinance or stay with the current mortgage, they are influenced by taste shocks4 that idiosyncratically affect their decision to repay. So, when nearly indifferent between refinancing and staying, approximately half of households will refinance and half will repay.
The quarterly government bond risk-free rate varies over time, evolving according to an AR(1) process. This is estimated from nominal, secondary market, three-month Treasury bill rates from the first quarter of 1954 to the second quarter of 2023 without detrending or accounting for the zero lower bound on interest rates. This gives quarterly persistence of 0.974 with a quarterly innovation of 0.0016 (0.64 percent annualized) and an unconditional mean of 0.0096 (3.90 percent annualized). From this quarterly process, I back out a yield curve and price two-year bonds, 10-year bonds and 30-year bonds using the internal rate of return (IRR).5
Lenders competitively price the bond, discounting using the risk-free government rate. Crucially, the price depends on how long the mortgage is expected to last, which depends on the endogenous refinance decisions of households. I use the IRR on the mortgage for a consistent comparison with mortgage debt. (Using the coupon gives almost identical results.)
Model Results
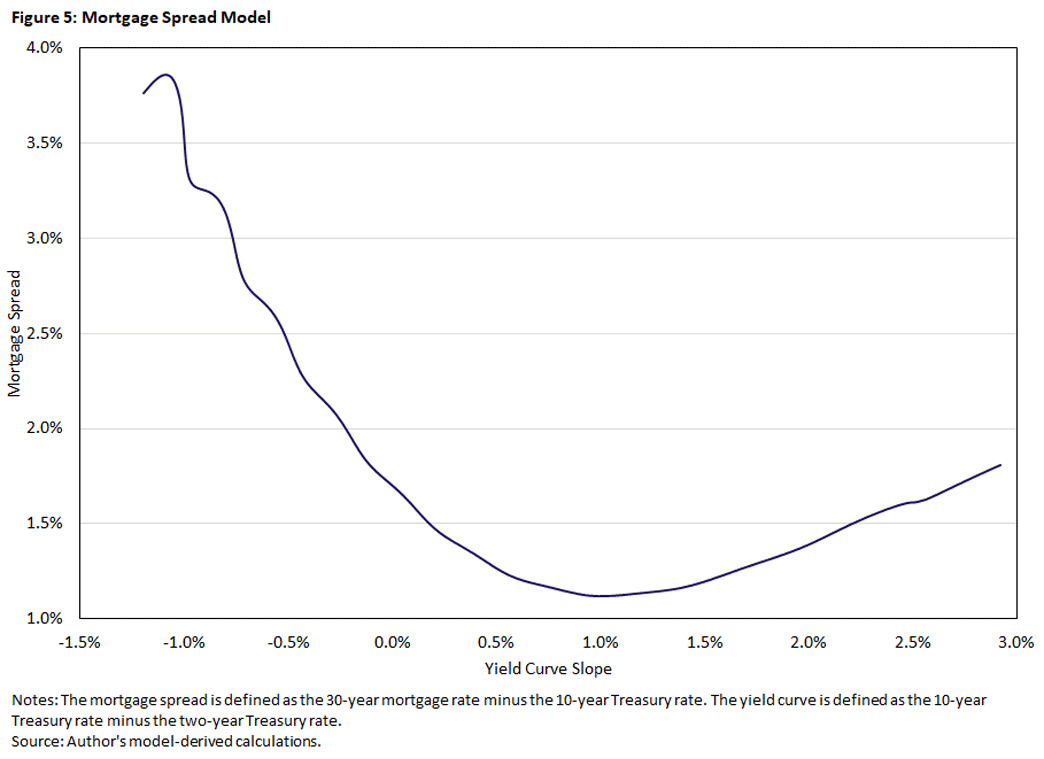
Figure 5 gives the model's equivalent of Figure 4, plotting the equilibrium relationship between the T10T2 yield curve slope and the mortgage spread.
The fit is exceptional, especially for such a simple and lightly parameterized model. When the yield curve is downward sloping (negative T10T2), there is a strong negative relationship between the mortgage spread and T10T2. This relationship flattens and reverses as the yield curve transitions to flat to upward sloping. And then there is a mild positive relationship between the spread and the T10T2 as the yield curve continues to steepen, as in the data.
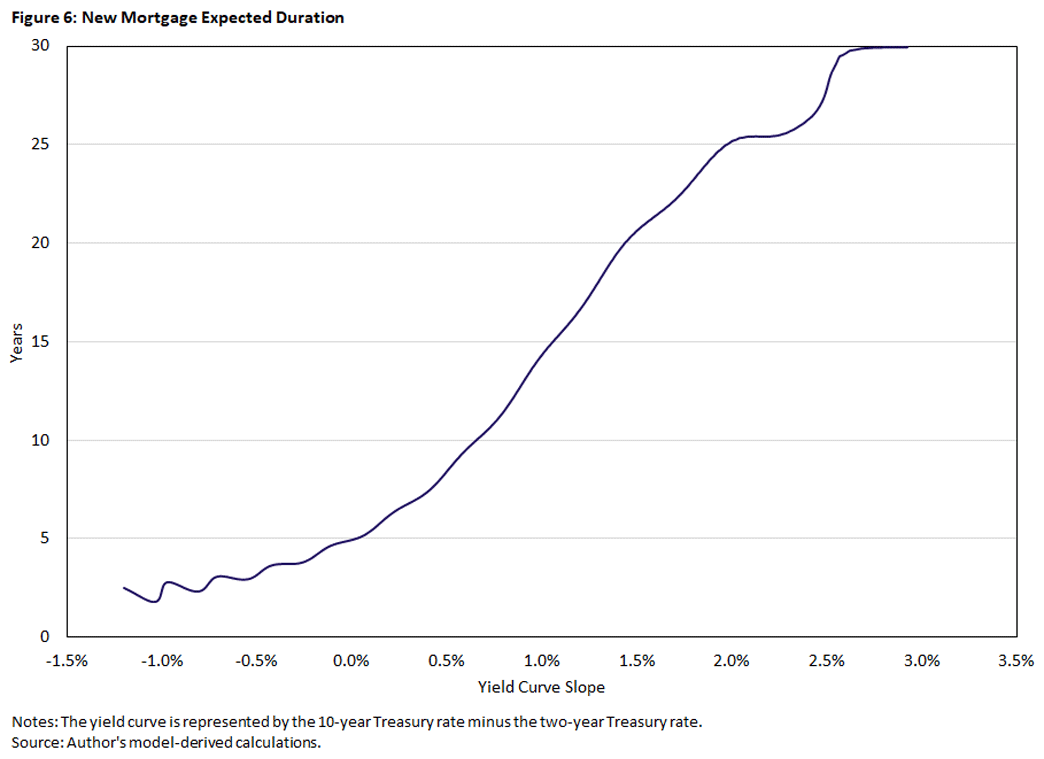
The model's mechanism operates through the mortgage market's endogenous changes in maturity. The expected duration of new mortgages is displayed in Figure 6.
As the yield curve inverts and becomes increasingly inverted, the expected duration falls to as low as one year. This makes the mortgage behave like (and be priced as) a short-duration asset, which in this case has a yield above the T10.
In contrast, as the yield curve slopes up and steepens, the expected duration rises monotonically to 10 years when the T10T2 is 0.7 percent. This is approximately where the mortgage spread attains its minimum, because this is where the mortgage duration is closest to the T10. As the yield curve continues to steepen, the mortgage duration rises to as much as 30 years when the T10T2 is 2.6 percent. This drives the mortgage spread up, because now the mortgage behaves more like a 30-year bond, which in this case has a yield higher than the T10.
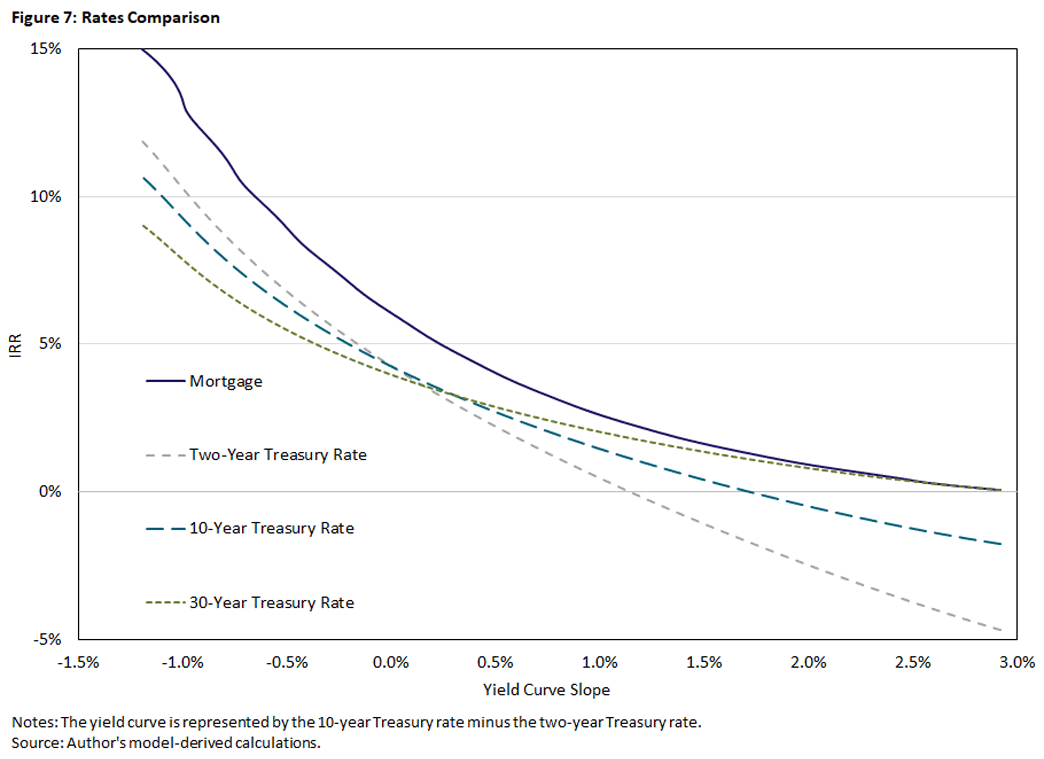
One can see this pattern explicitly in Figure 7: As the T10T2 gets very high, the mortgage rate converges to the 30-year Treasury (T30) rate.
Conclusion
The mortgage spread is sometimes viewed as a measure of market distortions. This explanation is intuitive but misleading. In this article, I argue that the reason mortgage spreads spike at the onset of recessions is because the expected duration of mortgages shortens drastically as the yield curve prices in a recession. This mortgage duration effect is evident in the data when considering the relationship between the T10T2 yield curve slope and the mortgage spread. The model validates this relationship, lending additional support for my interpretation of the data.
The importance of this brief for policymakers, researchers and financial analysts is that one should not use the mortgage spread as a gauge of financial market stress: Much of the variation is driven by refinancing behavior, not risk premia. Rather, in a downward-sloping yield curve environment, one should view the mortgage spread as a market expectation of increased refinance behavior in the near future.
This raises an additional question: What if these expectations disappoint? That is, what if lower future rates expected by the yield curve don't materialize, leaving households stuck with 7 percent mortgages they planned to refinance at 5.5 percent in 12 months? The implied financial burden could be large, on the order of several hundred dollars per month per homeowner. Investigation into this question should help policymakers navigate our current challenging economic environment.
Grey Gordon is a senior economist in the Research Department of the Federal Reserve Bank of Richmond. Many thanks to Alex Wolman for his comments on an earlier version of this brief.
The relationship extends back even further to 1976 (when the data begins), but I will focus on the stable-inflation period for this article. While some of the relationships weaken, the results in this article are robust to using a longer time span.
The 2019 paper "Understanding Mortgage Spreads" provides an excellent analysis of mortgage spreads. In that paper, prepayment is modeled in a general fashion as loading on multiple factors including the yield curve slope. The authors look at micro data to examine the moneyness of securities (whether the pecuniary value of refinancing would be very large, close to zero, or negative) and how mortgage spreads vary in that measure. They show that most of the aggregate variation in mortgage spreads is explained by prepayment risk. The approach in my article is closely related but simpler, examining a single prepayment factor — the slope of the yield curve — and showing that it is enough to explain most of the time-series variation. In general, the literature and public are well-aware that prepayment risk is a dominant factor in the mortgage spread. I am highlighting a particularly stark relationship between the mortgage spread and yield-curve slope.
This cost captures not only pecuniary costs of refinancing but nonpecuniary costs such as stress and inconvenience. It is a deadweight loss, is not transferred to the creditor and raises the expected mortgage duration without changing the shape of the mortgage spread.
The shock is Type I Extreme Value with parameter sigma = 0.002. I use it as a smoother, so it changes choice probabilities but does not show up directly in utility. But this assumption is immaterial for the results. (It could be treated structurally and affect utility.)
I use a technique common in the sovereign default literature, where an X-year bond is modeled as a bond with geometrically declining coupon payments that has a Macaulay duration of X years.
To cite this Economic Brief, please use the following format: Gordon, Grey. (August 2023) "Mortgage Spreads and the Yield Curve." Federal Reserve Bank of Richmond Economic Brief, No. 23-27.
This article may be photocopied or reprinted in its entirety. Please credit the authors, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.
Views expressed in this article are those of the authors and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.
Receive a notification when Economic Brief is posted online.