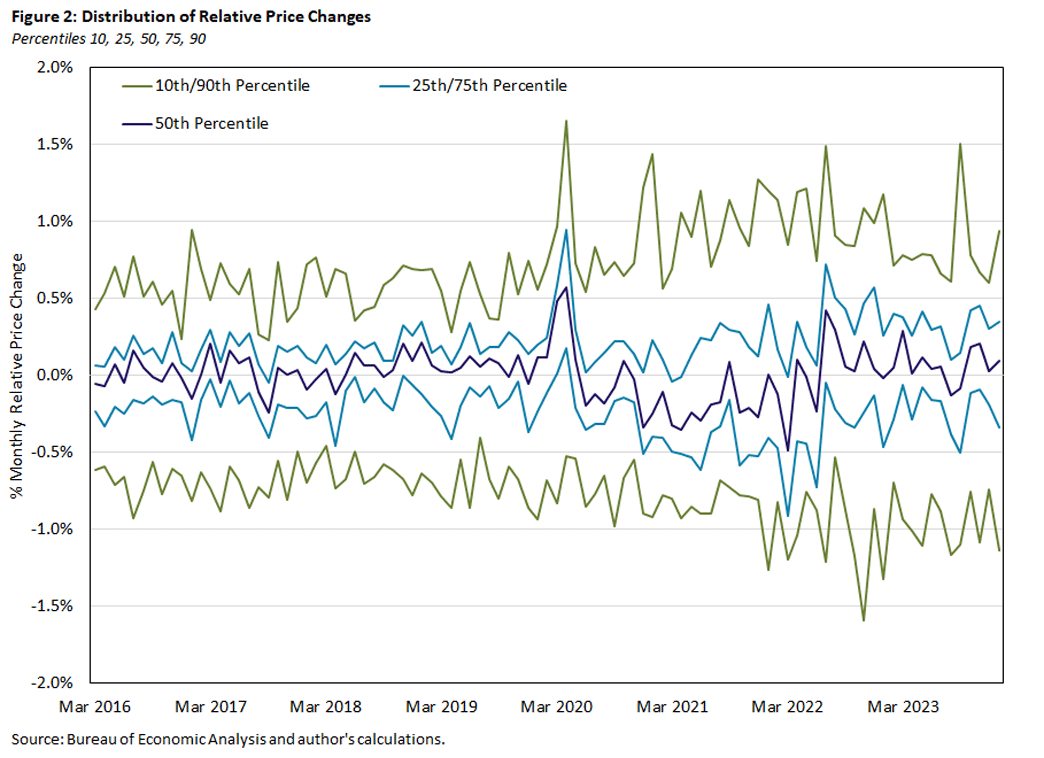Inflation and Relative Price Changes Since the Onset of the Pandemic

This article has two purposes. First, in the wake of the January PCE report, it provides an update on how inflation has behaved vis-a-vis the share of relative price increases, following up on my article from last spring and my Macro Minute blog post. Second, it provides some perspective on how the distribution of relative price changes has behaved since the onset of the pandemic, in comparison to the prior four-year period.

Previously, I discussed the fact that the 25-year period before the pandemic saw a stable, negative relationship between the monthly inflation rate and the monthly share of expenditures with relative price increases. A rough intuition for that relationship is as follows: The inflation rate was generally stable, and the monthly inflation fluctuations that did occur tended to be associated with large price changes for a small share of expenditures. For example, when the price of gasoline spiked in a particular month, gasoline might have been the only expenditure category experiencing a relative price increase (which is a nominal price increase greater than the inflation rate), and the inflation rate would have been high in that month. That is, a small share of relative price increases was associated with a high inflation rate.

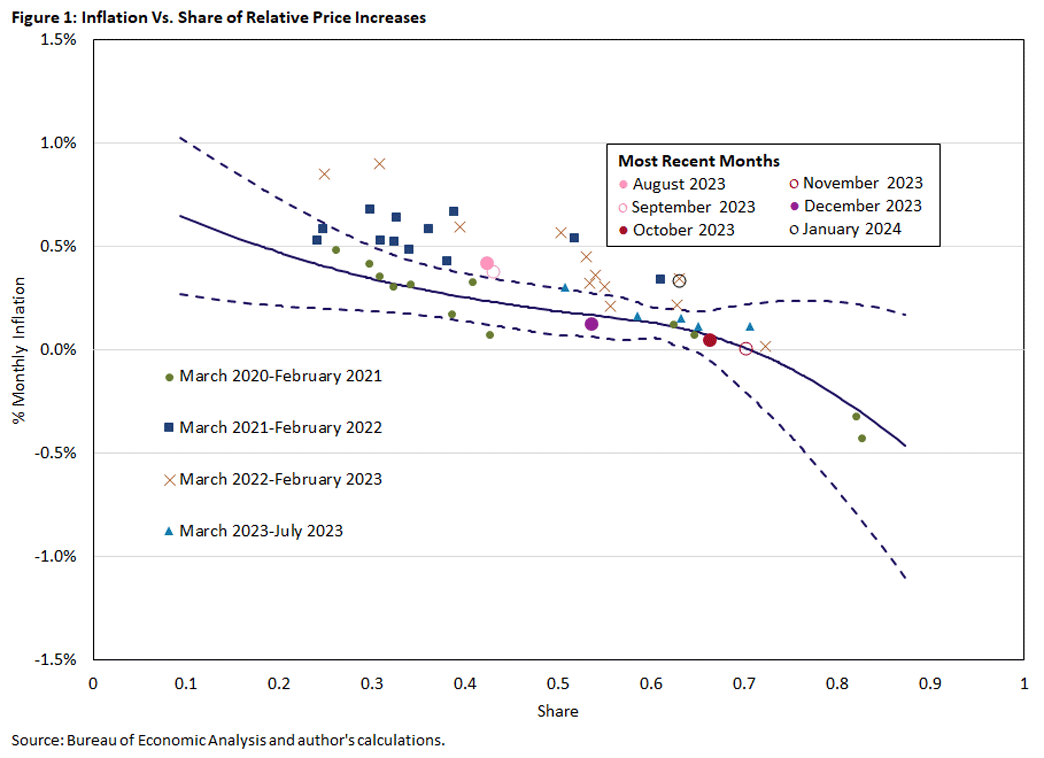
Figure 1 updates the relationship between monthly inflation and the share of relative price increases for PCE price data through January. The solid and dashed lines are based on a local polynomial regression using data from 1995 through 2019. They denote the predicted mean inflation rate and the two-standard deviation symmetric prediction interval around the mean. The points in the figure represent every month from March 2020 through January 2024.

Compared to the period from mid-2021 through early 2023, the last several months data have been encouraging: Conditional on the share of relative price increases (which can be thought of as a "real" variable), the inflation rate has behaved roughly as would have been expected based on the pre-pandemic relationship between those variables. That said, the January inflation report was not encouraging: Inflation was well above the pre-pandemic prediction interval conditional on the share of relative price increases.

The Relative Price Change Distribution Since the Pandemic

Figure 1 highlights a particular statistic from the distribution of relative price changes. We now turn to a more general discussion of how that distribution has behaved since the beginning of the pandemic.

Since the inflation rate is roughly the weighted average of all nominal price changes, where the weights are expenditure shares, it follows that the weighted average relative price change is always zero. As such, relative price changes are (as their name suggests) fundamentally "real" variables, and there is no necessary relationship between any aspect of the distribution of relative price changes and the inflation rate.¹ However, Figure 1 shows that there is in fact a relationship over the period 1995-2019, and a 1995 paper describes similar relationships in an earlier period.²

Nonetheless, for the time being we leave inflation in the background and focus on the distribution of relative price changes. Based solely on reading the business news, one would think that the distribution has looked quite different since the onset of the pandemic than it did previously.

Percentiles of the Distribution

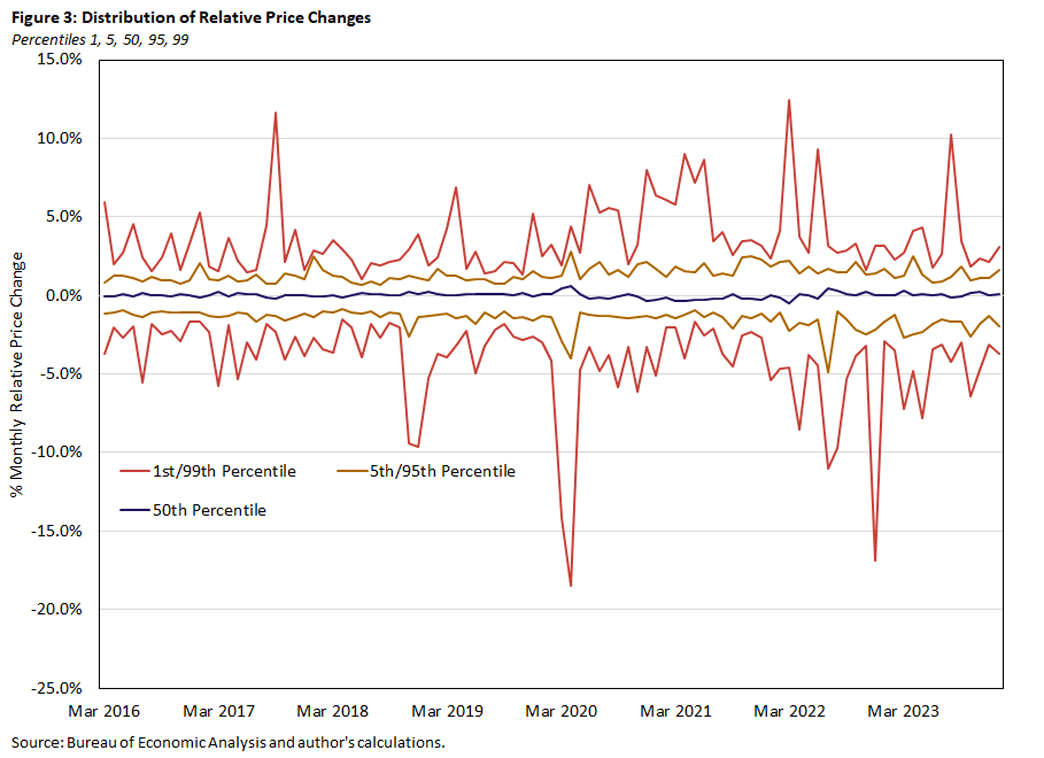
With PCE data available through January, we have 47 months of data since the onset of the pandemic in March 2020. In the figures below, we compare those 47 months to the previous four years of data, starting in March 2016. Figures 2 and 3 plot time series for percentiles of the distribution of relative price changes. Each month, we order relative price changes from lowest to highest, and the Xth percentile is the share of expenditures with a relative price change less than X.

For example, the green lines in Figure 2 are monthly values for the 10th and 90th percentiles of the distribution of relative price changes, the relative price changes for which 10 and 90 percent of expenditures have lower relative price changes, respectively.

Note that Figures 2 and 3 present material similar to that published by the San Francisco Fed. One difference is that we focus on relative price changes instead of nominal price changes. Certain statistics — such as the width of the interquartile range — will be the same whether one looks at relative or nominal price changes. In addition, we plot one-month price changes rather than 12-month price changes.

All of the series are volatile, but there seems to be a pattern of the distribution of relative price changes becoming more dispersed after March 2020. Because the mean of the distribution is zero, greater dispersion would be reflected in the low percentiles being more negative and the high percentiles being more positive.

Note that the distribution need not be symmetric — indeed, Figure 1 shows that it generally is not symmetric — so percentiles near the 50th are not informative about dispersion. Certain cases clearly indicate increased dispersion: For example, the green line in Figure 2 representing the 90th percentile shifted up starting in March 2020, and by early 2021 the other green line representing the 10th percentile (which is always negative) shifted down.

The Cumulative Distribution Function of Relative Price Changes, Pre- and Post-March 2020

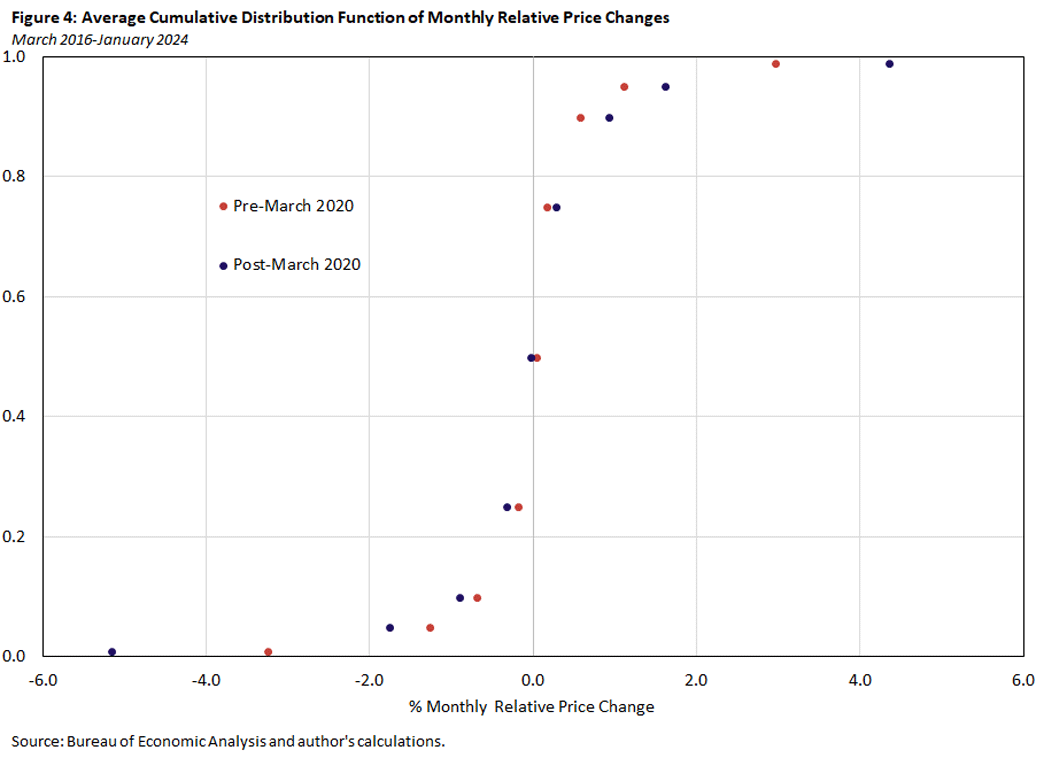
Figure 4 cuts through the noise of the previous figures to summarize the distributions before and after March 2020. For the two sample periods, it plots the average values across months of each percentile from Figures 2 and 3. That is, Figure 4 compares the cumulative distribution function (CDF) of relative price changes for the two samples.

The data that go into Figure 4 are the same as the data plotted in Figures 2 and 3. However, because it is a CDF, the values of the random variable (in this case, price changes) are plotted on the horizontal axis instead of the vertical axis, and the vertical axis corresponds to the probabilities ranging between zero and 1. For example, at a relative price change of zero, the CDFs for both periods take on a value close to 0.5. In other words, approximately half of the relative price changes are less than zero, as we would expect given that the mean relative price change is always zero.

The picture is striking: For every probability value on the Y-axis except for 0.5, the distribution is "stretched out" after February 2020 compared to before. That is, the X-value is lower for probabilities less than 0.5 after February 2020 and higher for probabilities greater than 0.5 after February 2020.

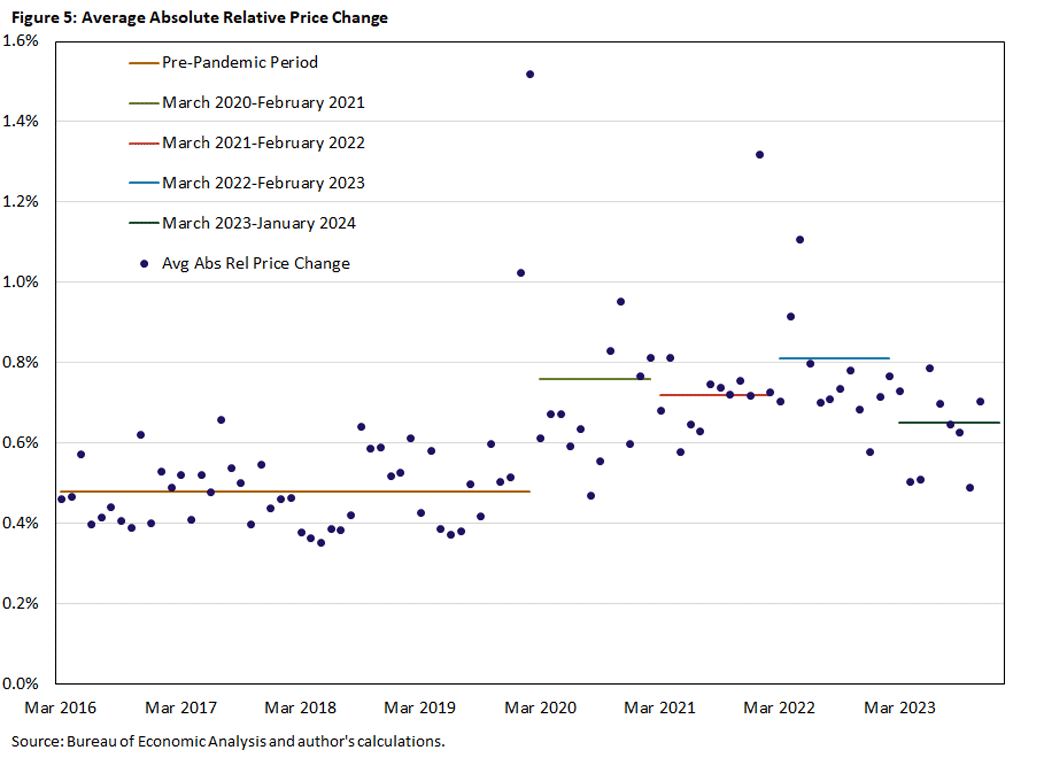
Average Absolute Relative Price Change

Figure 5 provides another perspective on the increased dispersion of relative price changes since the onset of the pandemic. It plots each months' value of the weighted average absolute relative price change. (Recall that the average relative price change is zero, so there would be nothing to see by plotting that; the absolute value provides a natural measure of dispersion.)

The message is unambiguous: Relative price changes have been larger after March 2020 than they had been in the previous four years. The horizontal lines in Figure 5 represent averages over five periods:

• The pre-pandemic period
• March 2020-February 2021
• March 2021-February 2022
• March 2022-February 2023
• March 2023-January 2024

In the most recent 11 months, relative price changes have become smaller but are still almost 50 percent higher on average than in the four years prior to the pandemic.

Conclusion: Bringing Inflation Back Into the Picture

We started by discussing inflation and the share of relative price increases. When inflation is generally stable, its monthly fluctuations are well explained by the monthly share of relative price increases. We then put inflation aside and focused entirely on the distribution of relative price changes, showing that relative price changes have tended to be larger since the beginning of the pandemic.

Can the high inflation that started in 2021 be explained by the properties of relative price changes? Without applying any theory, Figure 1 answers that question: From mid-2021 through early 2023, the high inflation cannot be explained by the share of relative price increases.

However, that answer restricts attention to one statistic of the distribution of relative price changes. More generally, theory tells us that inflation is an equilibrium outcome that reflects the interaction of monetary policy with real factors. My working paper "Relative Price Shocks and Inflation" — co-authored with Francisco Ruge-Murcia and currently being revised — suggests that factors driving relative prices may in fact account for much of the high inflation experienced in recent years. This is an active area of research, and we survey the literature in that paper.

Alexander L. Wolman is a vice president in the Research Department at the Federal Reserve Bank of Richmond.

To cite this Economic Brief, please use the following format: Wolman, Alexander L. (March 2024) "Inflation and Relative Price Changes Since the Onset of the Pandemic." Federal Reserve Bank of Richmond Economic Brief, No. 24-09.

This article may be photocopied or reprinted in its entirety. Please credit the author, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.

Views expressed in this article are those of the author and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.