Residual Seasonality in Monthly Core Inflation
At the end of 2023, three-month average core CPI inflation came in at 3.6 percent annualized. However, January and February 2024 core CPI inflation came in at 4.8 percent annualized. Given the volatility in monthly inflation numbers, one should not take too much signal from one or two months of data. Furthermore, the possibility has been raised that there is a regular but transient inflation uptick early in the year, even in seasonally adjusted data. In this article, I show that, for the last 20 years, there is no statistical evidence for this kind of residual seasonality in monthly core CPI or PCE inflation.
At its January meeting, the Federal Open Market Committee (FOMC) stated that it would need to gain "greater confidence that inflation is moving sustainably toward 2 percent" before it would be appropriate to cut the policy interest rate. However, following a substantial disinflation in the last quarter of 2023, core inflation came in noticeably higher in the first two months of 2024.
Given the volatility in monthly inflation numbers, one should not read too much into one or two months of data. But some have argued that one should read even less into higher inflation early in the year because of residual seasonality. That is, inflation (even in seasonally adjusted data) regularly experiences an early-year uptick that does not persist over the rest of the year. In this article, I show that, for the last 20 years, there is no statistical evidence for residual seasonality in monthly core consumer price index (CPI) or personal consumption expenditures (PCE) inflation.
Observing Seasonality
Many economic time series display seasonal patterns related to weather or holidays. For example, construction employment tends to fall in winter months, and retail sales tend to increase between Thanksgiving and Christmas.
An extreme case is overall payroll employment, which has fallen by about 3 million every January for the past 20 years. To put that number in perspective, in mid-2009 (during the depths of the Great Recession), payroll employment declined by about 6.7 million on a year-over-year basis. That this recurring January employment decline does not receive much attention reflects the fact that the decline is regularly reversed from February to April.
Such seasonal patterns in economic time series obscure the month-to-month changes one is often interested in. Statistical agencies therefore seasonally adjust the time series, removing the seasonal effects and creating a distinction between initial not-seasonally adjusted (NSA) series and the seasonally adjusted (SA) series. "Residual seasonality" then refers to a phenomenon where seasonal patterns remain in the SA series.
Seasonality in Core Price Inflation
We now illustrate the effects of seasonal adjustment for the monthly inflation rate in core CPI and the price index for core PCE. The CPI is produced by the Bureau of Labor Statistics (BLS) and serves not only as a measure for cost of living but also as an input for price indexation in government spending programs, such as Social Security payments. The PCE is produced by the Bureau of Economic Analysis (BEA) as an input for the National Income and Product Accounts (NIPA).
Both price indexes are expenditure-weighted averages of component price series that have many common elements, but they also differ substantially in some respects. One major difference is that the CPI is a fixed-weight price index (meaning that the expenditure weights are not adjusted frequently), whereas the PCE is a chain-weight index (meaning that monthly expenditure weights reflect current nominal consumption expenditures). Therefore, the PCE better reflects changes in cost of living, since it accounts for household substitution effects in response to relative price changes. For example, if households respond to price increases on beef by substituting chicken, the PCE takes this substitution into account. This is one of the reasons PCE inflation is the FOMC's preferred inflation measure.
We focus on the core price indexes, which exclude prices related to food and energy as they are two very volatile price components of overall consumer spending. Frequently, price changes in food and energy are reversed within a short period, and excluding food and energy makes core price inflation a better predictor of future inflation.
In all that follows, we calculate monthly inflation at annual rates. A simple seasonal adjustment procedure for monthly data is to compute the symmetric 13-month moving average (MA) of the NSA series — that is, the average over the period from six months prior to a given month to six months after. Differences between the NSA and the SA series tell us the size of the seasonal effect in each month.
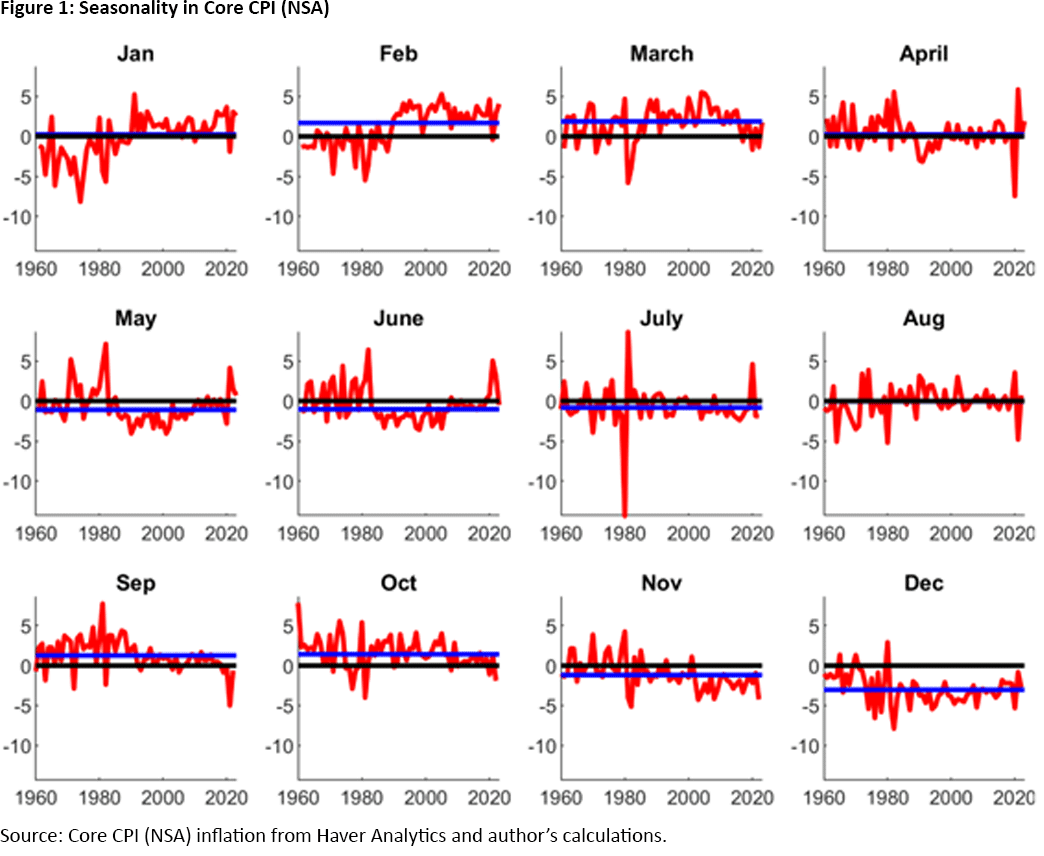
Figure 1 illustrates this procedure for the monthly inflation rate of core CPI from 1960 to 2023. We plot the deviations of each month's NSA inflation rate from the corresponding 13-month MA value for that month. We also plot the mean deviation of NSA inflation from its MA value for the full sample period, shown via the blue lines.
Clearly, NSA inflation is higher on average than SA inflation in March and is lower in December. But it is also true that the deviations are quite large and volatile. We would therefore like to have a method that tells us if the average deviation for a month is meaningfully different from zero. Also, the panels for January and February suggest that seasonal patterns change over time: The seasonal effect in NSA inflation switched from negative before 1990 to positive since.
Residual Seasonality
To get a better understanding of residual seasonality in the monthly inflation series for core price indexes, we now calculate the monthly means and standard deviations of a series' seasonal residuals defined (as above) as the difference between the series and its 13-month symmetric MA. We display these means and standard deviations in Table 1 for core CPI (NSA), core CPI (SA) and core PCE (SA). We consider the sample period from 2000 to 2023.
| Core CPI (NSA) | Core CPI (SA) | Core PCE (SA) | ||||
|---|---|---|---|---|---|---|
| Month | Mean | Standard Dev | Mean | Standard Dev | Mean | Standard Dev |
| Jan | 1.35 | 1.36 | 0.10 | 1.06 | 0.72 | 1.19 |
| Feb | 2.97 | 1.27 | -0.38 | 1.38 | -0.02 | 0.60 |
| March | 2.16 | 1.86 | -0.19 | 2.25 | -0.05 | 0.82 |
| April | 0.25 | 2.22 | -0.05 | 1.28 | 0.19 | 1.60 |
| May | -0.77 | 1.71 | 0.21 | 1.42 | 0.03 | 0.69 |
| June | -0.45 | 1.77 | 0.14 | 1.48 | 0.05 | 0.82 |
| July | -0.95 | 1.42 | -0.08 | 1.50 | 0.02 | 1.06 |
| Aug | 0.04 | 1.57 | 0.02 | 0.94 | -0.24 | 0.92 |
| Sept | 0.20 | 1.35 | 0.23 | 1.06 | -0.40 | 1.91 |
| Oct | 1.00 | 1.34 | 0.05 | 1.00 | 0.39 | 1.82 |
| Nov | -2.24 | 1.27 | -0.27 | 0.98 | -0.28 | 0.90 |
| Dec | -3.35 | 1.12 | 0.26 | 1.36 | -0.25 | 0.86 |
| Source: Core CPI and PCE inflation from Haver Analytics and author's calculations. | ||||||
The first two columns cover core CPI (NSA). There appear to be four months with strong seasonals:
- February and March have positive mean residuals above 2 percentage points.
- November and December have negative mean residuals below -2 percentage points.
However, only the December mean seasonal would qualify as significantly different from zero if we used the criterion that the absolute value of the mean had to be at least twice the standard deviation.1
The next two columns cover core CPI (SA) as adjusted by the BLS. Now the means of all monthly residuals are quite a bit smaller than their standard deviations, and it looks as if the BLS's SA procedure does a good job at removing seasonals.
The last two columns cover core PCE (SA) as adjusted by the BEA. The monthly means and standard deviations for core PCE (SA) inflation residuals are of a similar magnitude as for the CPI, except for January. But even for January, the mean residual is quite a bit smaller than its standard deviation.
Two comments on the SA series provided by the BLS and BEA. First, they both use more sophisticated techniques than the simple symmetric MA I have used so far to seasonally adjust data. A problem with the symmetric MA is that, at the end of the sample, you don't yet have information on the next six months to make the seasonal adjustment. One can specify and estimate a statistical model that includes seasonal effects for the time series and then use the model's forecast for the missing observations at the end of the sample. But once one has fitted a time-series model, the symmetric MA might not be the most efficient way to eliminate seasonal effects from the time series. All these issues are addressed in the procedures that the statistical agencies use to seasonally adjust data. The BLS and BEA use essentially the same procedures.
Second, the BEA only publishes monthly data for the core PCE index that are already seasonally adjusted, while NSA core PCE data are available at a quarterly frequency. In fact, before 2018, the BEA only published SA NIPA data, and there was some concern about residual seasonality in these data. In particular, there was evidence suggesting negative first quarter seasonality in GDP despite the GDP series already being seasonally adjusted. The BEA subsequently revised its SA procedures and has published NSA and SA data for the main NIPA components — including the core PCE price index — at a quarterly frequency since 2018. These improvements have apparently reduced the scope for residual seasonality in GDP and its components.2
Tests for Residual Seasonality
So far, we have used informal methods to investigate if there is residual seasonality in monthly core inflation. We now use three formal statistical tests for the presence of seasonality.3 We test the three core inflation series for seasonality over three sample periods — 1960-1979, 1980-1999 and 2000-2023 — because seasonal patterns may change over time, as we have noted.
Stable Seasonals
We first test for the presence of stable seasonals. Essentially, we test for non-zero additive effects that are constant over the years but different across months. This is also called a Wald test, and we display the p-values for this Wald test in Table 2.
| Subsample | Core CPI (NSA) | Core CPI (SA) | Core PCE (SA) |
|---|---|---|---|
| 1960-1979 | 0.00 | 0.32 | 0.17 |
| 1980-1999 | 0.00 | 0.86 | 0.00 |
| 2000-2023 | 0.00 | 0.51 | 0.12 |
| Source: Core CPI and PCE inflation from Haver Analytics and author's calculations. | |||
In essence, the p-value tells us the probability that the Wald test statistic we calculate for a sample is as large as observed in a world where this kind of seasonality is not present. Smaller p-values cast more doubt on the hypothesis of no seasonality.
The probability of such an event for core CPI (NSA) is zero for all three sample periods. This provides very strong evidence that monthly inflation for core CPI (NSA) contains seasonal effects. On the other hand, the p-values for monthly inflation of core CPI (SA) are all quite large, so we can be confident that the BLS's seasonal adjustment procedures have removed the seasonal components of core CPI (NSA).
Finally, the evidence on monthly core PCE (SA) inflation is mixed. For the period before 1980 and the recent period since 2000, the p-values are large, and we would reject the hypothesis of additive residual seasonality. However, for the period 1980-1999, we have a p-value of zero and would accept the possibility of residual seasonality.4
Unstable Seasonals
We have noted that seasonal patterns can change over time, which we'll call unstable seasonals. The CH test proposes a particular pattern for this drift in seasonal factors, namely a random walk. In Table 3, we report the p-values for this CH test.
| Subsample | Core CPI (NSA) | Core CPI (SA) | Core PCE (SA) |
|---|---|---|---|
| 1960-1979 | 0.37 | 0.70 | 0.79 |
| 1980-1999 | 0.23 | 0.94 | 0.60 |
| 2000-2023 | 0.00 | 0.40 | 0.32 |
| Source: Core CPI and PCE inflation from Haver Analytics and author's calculations. | |||
The p-value is now the probability that we observe a CH statistic greater or equal to the one we calculate for the sample if the additive seasonals are not drifting. (Note that the test allows for non-zero constant seasonals.) As with the previous test, smaller p-values provide evidence against the hypothesis of stable seasonality. For core CPI (NSA) inflation, we would reject stable seasonality only for the 2000-2023 subsample where the p-value is zero. In contrast, we would not reject the hypothesis of stable seasonality in any of the three samples for core CPI (SA) and core PCE (SA).
Drifting Seasonal Factors
Finally, we test for the joint hypothesis that the seasonal factors are not drifting and that they are constant at zero. We report the p-values for this joint Wald test and CH test in Table 4.
| Subsample | Core CPI (NSA) | Core CPI (SA) | Core PCE (SA) |
|---|---|---|---|
| 1960-1979 | 0.00 | 0.32 | 0.17 |
| 1980-1999 | 0.00 | 0.87 | 0.00 |
| 2000-2023 | 0.00 | 0.51 | 0.12 |
| Source: Core CPI and PCE inflation from Haver Analytics and author's calculations. | |||
The p-value is now the probability that we observe a joint Wald and CH statistic that is greater or equal to the one we calculate for the sample if the additive seasonals are not drifting and are constant at zero. The results are essentially the same as for the simple Wald test. We reject the absence of seasonality for core CPI (NSA) for all sample periods. We accept the absence of residual seasonality for core CPI (SA) for all sample periods. And we reject the absence of residual seasonality for core PCE (SA) only for the period 1980-1999.
Before we conclude, we want to address two additional issues related to seasonally adjusted data. First, SA series are frequently revised at the end of the sample since they are based on symmetric filters calculated using forecasts of the NSA series. Thus, for a comprehensive assessment of the SA process, one might want to test for residual seasonality using the data series that are available in real time.
Second, monthly CPI inflation is very noisy, which might hide underlying seasonality at quarterly frequencies. For this to matter, though, the monthly error terms would have to be correlated in a very particular way: within a quarter. In an accompanying note to this article, we confirm that the evidence on residual seasonality for monthly and quarterly real-time data for core CPI and PCE inflation is consistent with what we have shown in this article.
Conclusion
We have looked at seasonal patterns in monthly inflation rates for core CPI (NSA and SA) and core PCE (SA). For the period 2000-2023, we find statistically significant evidence of seasonality in core CPI (NSA) but not in core CPI (SA). That is, the BLS has successfully deseasonalized core CPI (NSA). We find some evidence for residual seasonality in core PCE (SA) for the years prior to 2000 but no evidence of residual seasonality for the period 2000-2023. Thus, residual seasonality is not a good enough reason to discount unusually high inflation early in the year.
Andreas Hornstein is a senior advisor in the Research Department at the Federal Reserve Bank of Richmond. The author thanks David Ramachandran for research assistance and Jonathan Wright for providing his code to test for seasonality in time series.
If the monthly seasonals were normally distributed with mean zero and the calculated monthly standard deviation, then the probability that the absolute value of the calculated mean is more than two standard deviations is about 5 percent.
For example, see the 2018 paper "Seasonal Adjustment of NIPA Data" by Jonathan Wright and the references therein to the literature on residual seasonality in GDP and its components.
The tests include a standard Wald test for stable constant seasonals and a test for time-varying seasonals based on the 1999 paper "Are Seasonal Patterns Constant Over Time? A Test for Seasonal Stability" by Fabio Canova and Bruce Hansen as implemented by the previously cited paper "Seasonal Adjustment of NIPA Data." I would like to thank Jonathan Wright for making his code available to me.
As part of the discussion of residual seasonality in NIPA data, the 2014 paper "Mitigating Residual Seasonality While Preserving Accounting Relations in Hierarchical Time Series" by Tucker McElroy, Osbert Peng and Baoline Chen and the 2019 article "Residual Seasonality in Core Consumer Price Inflation: An Update" by Ekatarina Peneva and Nadia Senee argued that there was residual seasonality in core PCE inflation before 2019.
To cite this Economic Brief, please use the following format: Hornstein, Andreas. (May 2024) "Residual Seasonality in Monthly Core Inflation." Federal Reserve Bank of Richmond Economic Brief, No. 24-13.
This article may be photocopied or reprinted in its entirety. Please credit the author, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.
Views expressed in this article are those of the author and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.
Receive a notification when Economic Brief is posted online.