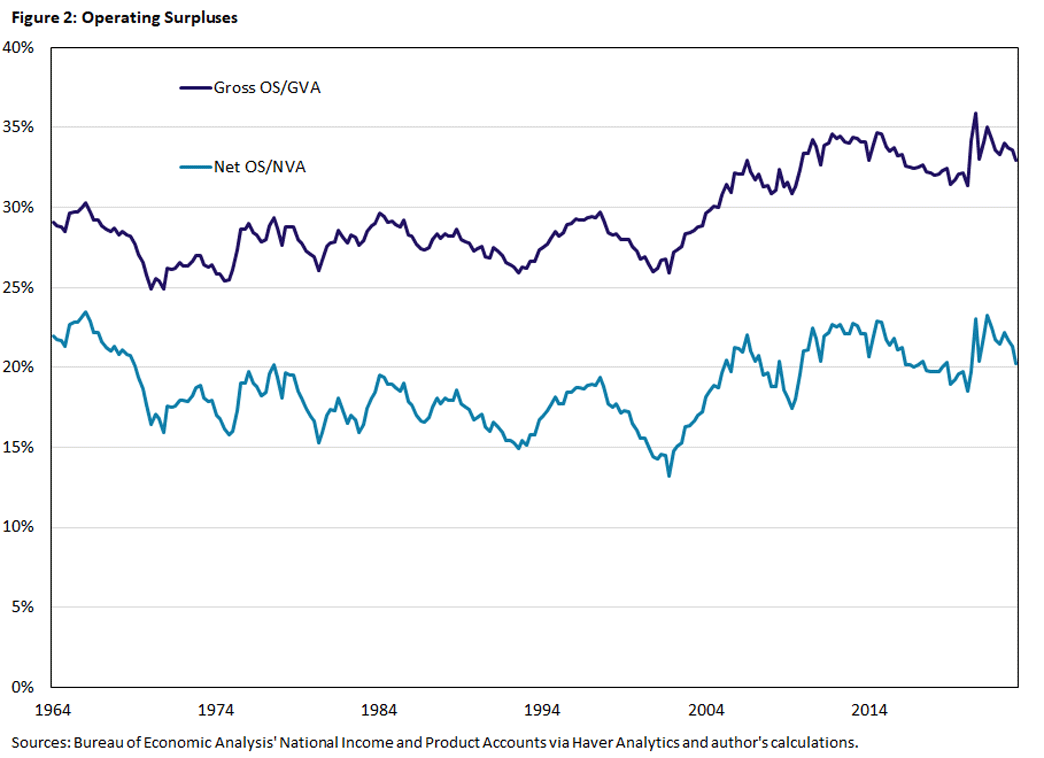Profits and Inflation in the Time of COVID
Following the onset of the COVID pandemic in 2020, inflation accelerated in 2021-22 and peaked at roughly 7 percent in mid-2022. This was an inflation rate not seen since the early 1980s. Among the many accounts of this increase that have been introduced, one attributes the increase to firms being greedy and exploiting supply chain disruptions to raise their prices excessively. In this article, I first argue that a frequent piece of evidence in support of "greedflation" — the increased share of gross operating surplus in the nonfinancial corporate business (NFCB) sector — is not that informative about profits. I then construct an alternative measure of profits — the price-cost markup — using standard measures and show that its contribution to inflation in the NFCB sector was rather small.
Popular press, bloggers and even policymakers have pointed to excessive profit-taking as a source of the surge of U.S. inflation in 2021-22 and more recently in Europe. This comes under the header of "greedflation."1
But if producers always seek to maximize profits, why would they raise prices excessively in the years following the pandemic? One possible reason is that the pandemic environment and its associated supply chain problems made it easier for firms to do that. But what does it mean for firms to raise prices excessively?
Following the greedflation commentary, one may get the impression that it is obvious what constitutes "profits." But it is not that obvious from an economist's perspective. The most popular piece of evidence in support of greedflation is the increased share of "profit" in corporate gross value added (GVA). This comes from the National Income and Product Accounts (NIPA), titled "corporate profits after tax with inventory valuation adjustment and capital consumption adjustment."
But this measure conflates economic profits with payments to capital, an input to production. Similar to labor (the other input to the creation of value added), capital is paid a return. Economic profits are then the excess of revenue over competitive payments to inputs. But since we do not have a good measure of payments to capital, we don't have a good measure of payments to all inputs and, therefore, of profits.
When firms have market power, they generate profits by pricing their output above cost. Thus, one way to measure whether firms are exploiting their market power is to look at the behavior of markups, or the excess of price over marginal cost. The New Keynesian theory of inflation (a popular applied monetary theory) is all about firms with market power that set their prices above marginal cost but also can adjust these prices only infrequently.
In this theory, nominal demand shocks can have real effects because average markups can move when prices are sticky. People working with this theory therefore developed an interest in measuring changes in markups. We apply some of these methods to construct measures of markup changes since 2020. We find that the contribution of markup changes to inflation was quite small.
In the following, we first review the standard evidence in support of the role of greedflation, namely the contributions of income components to inflation in the U.S. nonfinancial corporate business (NFCB) sector. We then briefly review the basic New Keynesian model of inflation. Finally, we calculate measures of markup changes based on the 2020 paper "The Cyclical Behavior of the Price-Cost Markup."
The Nonfinancial Corporate Business Sector
The discussion of the contribution of increased profit-taking to inflation is frequently focused on the NFCB, for several reasons:
- The data are readily available through the U.S. Bureau of Economic Analysis (BEA) as part of the NIPA.
- Profits are frequently defined as the part of the sector's GVA that is not paid to labor, and we are relatively confident that labor compensation is well measured in the NFCB sector.
- We want to know what accounts for the behavior of prices, and we are relatively confident that prices are well measured in the NFCB sector.
We assume that labor compensation in the corporate sector of the economy is better measured than in the noncorporate sector because it is not obvious how proprietors' income in the latter should be treated. Some of that income may well represent compensation for the labor services a proprietor provides to his/her firm, but another part may represent compensation for the use of capital owned by the proprietor.
We also assume that prices in the nonfinancial sector are better measured than in the financial sector. The nonfinancial sector produces goods and nonfinancial services, whereas the financial sector produces financial services. If we were to rank how confident we are in the quality of the price indexes we construct for the goods produced in the U.S. economy, we would put goods first, nonfinancial services second and financial services third.
The NFCB sector represents a large part of the U.S. economy, so it may well be informative for the overall economy. In 2020, GVA in the NFCB sector represented about 85 percent of corporate business GVA, 66 percent of total business GVA and 50 percent of overall GDP. Furthermore, price inflation in the NFCB sector since 2020 is comparable to price inflation in the overall economy and personal consumption expenditure (PCE) inflation in particular. The latter is the price index monetary policymakers (that is, the Federal Open Market Committee) target at 2 percent.
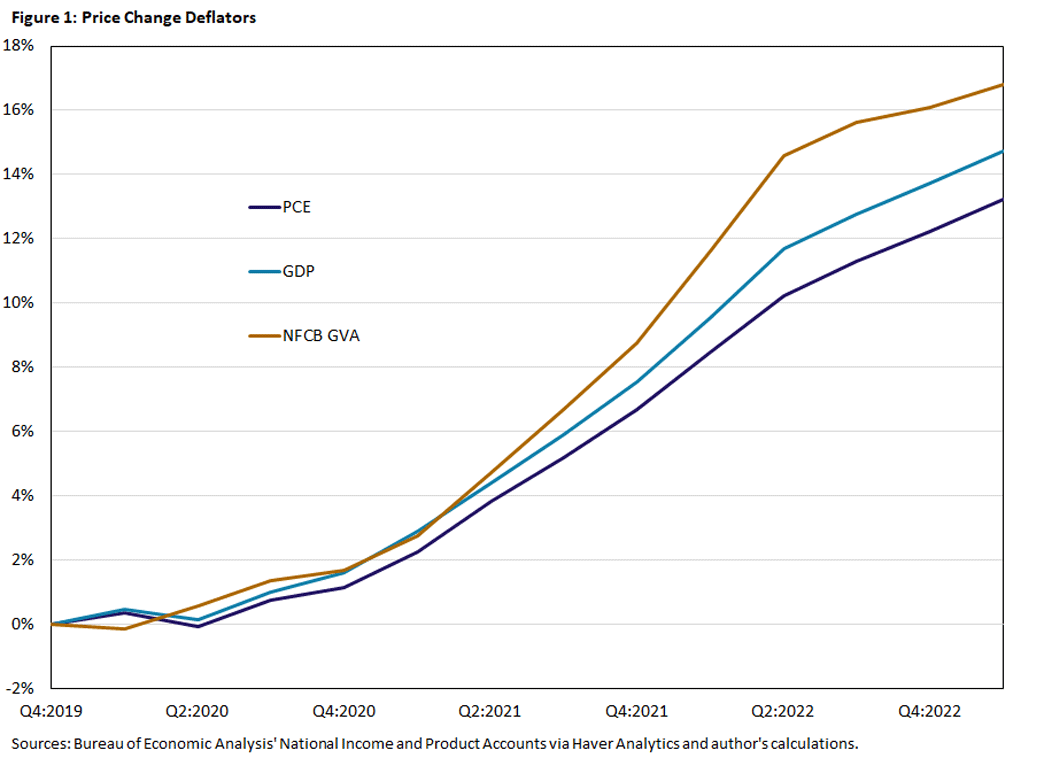
Figure 1 plots the cumulative change in prices since the fourth quarter of 2019 for the price deflators of the NFCB sector's GVA, aggregate gross domestic product (GDP) and aggregate PCE.
As we can see, the price changes are comparable: Increases in the three price indexes ranged from 13 percent to 17 percent over three years, roughly 4 percent per year or twice the rate targeted by the FOMC. The NFCB sector price index increased the most, the PCE price index increased the least, and the rate of price increase accelerated in 2021 for all three indexes.
Profits and Inflation in the NFCB Sector
GVA is the sectoral analogue to aggregate GDP: It reflects the value of final goods produced and the payments to primary inputs to production. We have a measure of nominal GVA from the production side, a decomposition of GVA on the income side and a price index of the final goods produced by the sector. Real GVA is nominal GVA deflated by the price index.
Nominal GVA on the production side is the value of nominal gross output less the value of intermediate inputs purchased. Nominal GVA on the income side lists payments to primary inputs and taxes/subsidies associated with the creation of GVA. The big components are taxes net of transfers associated with doing business, labor compensation and the gross operating surplus (GOS). Note that we can view the GOS as the residual after we subtract taxes and labor compensation from the GVA that we obtained from the production side. The BEA calculates depreciation associated with the use of capital in the NFCB sector. Subtracting depreciation from the GOS, we obtain the net operating surplus (NOS), which can be split into corporate income taxes and a component called "net profits after taxes."
Figure 2 plots the GOS as a share of GVA and NOS as a share of net value added (NVA), that is, GVA less depreciation.
As we can see, both shares were volatile prior to 2000 but displayed no apparent trend. But since 2000 these shares have increased (more so for GOS than NOS), and both shares jumped drastically early in the pandemic. After 2000, both surplus shares saw averages of almost 5 percentage points more relative to their pre-2000 averages. This fact has generated a large economics literature mostly attributing the increased share to an increase in market power and higher profit rates.2 Looking at the 2020 pandemic, the surplus share appears to increase by close to 3 percentage points. This surplus share jump has been frequently attributed to firms exploiting pandemic-induced market disruptions and raising their prices, resulting in profit-driven excess inflation (or "greedflation").3
Next, we want to account for the change in the NFCB sector price deflator through changes in its income/cost side. For this purpose, we divide the income components of nominal GVA by real GVA. That is, we get the cost components per unit of real GVA. These unit cost components add up to the (unit) price index.
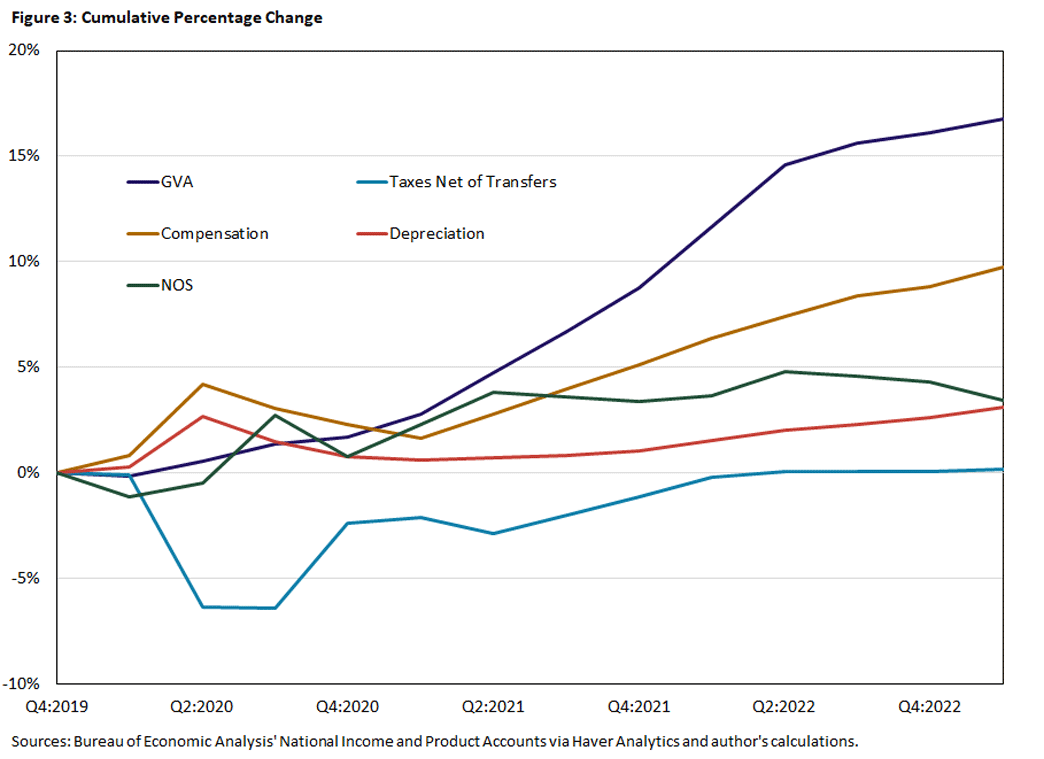
In Figure 3, we plot the cumulative percentage change of the GVA price deflator and the unit cost components since the fourth quarter of 2019.
As we can see, changes in the GOS (that is, NOS plus depreciation) contributed substantially to the 6-percentage-point price increase in the first 1.5 years of the pandemic (the second quarter of 2020 through the third quarter of 2021). In fact, almost all the cumulative price increase can be attributed to an increase in the GOS, with changes in business taxes and labor compensation offsetting each other. Over the next 1.5 years, prices increased by another 10 percentage points, but the changes in the GOS share contributed only 1 percentage point to that increase.
For the full period, changes in the GOS accounted for about one-third of the cumulative price increase. This is about twice the average contribution of changes in the GOS to annual inflation over the period 1964-2019, as seen in Table 1.
| Table 1: Income Sources of NFCB Inflation 1964-2019 |
|
|---|---|
| Income Component | Contribution |
| Business Tax Net of Subsidies | 3% |
| Labor Compensation | 81% |
| Depreciation | 14% |
| NOS | 2% |
| Note: This displays the average contribution of the main income components to year-over-year inflation of the GVA deflator in the NFCB sector. | |
What should we conclude from this? In an accounting sense, the increased share of the GOS was an important source of inflation for this period, but how much of that reflects profits? About half of the GOS contribution reflects increased depreciation, which clearly does not represent profits. The other half of the GOS contribution comes from the NOS, which may include profits but also includes payments to capital.
From an economist's perspective, capital and labor are the primary inputs to production of GVA. As such, the rental rate of capital (that is, the price of capital services) is part of the marginal cost of production. A competitive firm is assumed to price its product at marginal cost, whereas a firm with market power prices its product at a markup above marginal cost. Profits, then, reflect the excess of price over marginal cost.
The problem with capital is that a firm typically owns the capital used in production and does not hire the capital services in a market. Thus, we do not observe the price paid for the use of capital services. Economists have developed methods to calculate an implicit price for capital services, but their application is not always straightforward, which makes the calculation of firm profits a difficult enterprise.
Nevertheless, New Keynesian models have become a popular model of inflation over the last 30 years, and these models are predicated on the assumption that price-setting firms have market power. So, maybe we can use some of what we learned from these models to study the contribution of profit-taking to inflation.
The Markup: Market Power in New-Keynesian Models of Inflation
In the basic New Keynesian model, profit-maximizing firms are assumed to have market power in their product markets but not in their input markets. Since firms are competitive in their input markets, they take their input prices as given and minimize the cost of producing a given output quantity. This gives rise to a cost function that increases with the quantity produced. Since firms have market power in their output market (represented by a downward-sloping demand for their product), the marginal revenue from an additional unit sold declines with total sales. Firms maximize profits by equating the marginal revenue from one more unit sold with the marginal cost of producing that additional unit. The resulting profit-maximizing price is a markup over marginal cost. Usually, one assumes a particular functional form for firms' demand functions such that the markup is constant.
But this is not the complete New Keynesian model of inflation. What generates real effects from nominal disturbances in these models is the assumption that prices are "sticky." This means that a firm can adjust its price only infrequently, and after adjustment the firm must stick with the price for some time and fulfill any forthcoming demand for its product.
Furthermore, price adjustment is spread out across firms, as not all firms adjust their prices at the same time. Thus, during the time a firm's price is fixed, its marginal cost may change. (That is, its price-cost markup may change.) And since price adjustment is not synchronized across firms, the average markup may change in a systematic fashion.
The combination of profit-maximizing price setting and sticky prices gives rise to a monetary non-neutrality. For example, in response to an expansionary monetary shock, all firms want to increase their prices, but only some can. Because of the incomplete price adjustment, aggregate output and employment increase. Inflation, real wages and marginal cost also increase, but aggregate markups and profits decline. So, for monetary shocks, markups and inflation are negatively correlated.
It would then seem useful to check this prediction of the New Keynesian theory. And the 2020 paper "The Cyclical Behavior of the Price-Cost Markup" does that. The authors show how to calculate price-cost markups, and we follow their approach and calculate the contribution of markup changes to pandemic inflation.
Measures of the Markup
We will now describe how the paper's authors calculated changes in markups and show how these changes contributed to inflation post-2019.
We start with prices (p) as a markup (m) over marginal cost (c), with the equation: p=m*c. This is essentially just a definition. We can calculate the rate of change (D) of each variable and obtain Dp=Dm+Dc. Thus, as a matter of accounting, inflation is the sum of changes in the markup and marginal cost. The important thing is to measure changes in the markup.
To talk about the markup, we will have to get more specific about marginal cost. Suppose the firm can hire labor (h) in a competitive market at a fixed wage (w). Let MPH denote the marginal product of labor (that is, the additional output [y] from hiring one more unit of labor). Then, the marginal cost of producing one more unit of output is c=w/MPH.
With a little more algebra, we can rewrite the price-cost markup equation as m=eH/sH where eH is the elasticity of output with respect to labor (that is, the percentage increase of output implied by a one percent increase of labor) and sH= w*h/p*y is the revenue share of labor. We now have an expression for the change in the markup: Dm=DeH-DsH
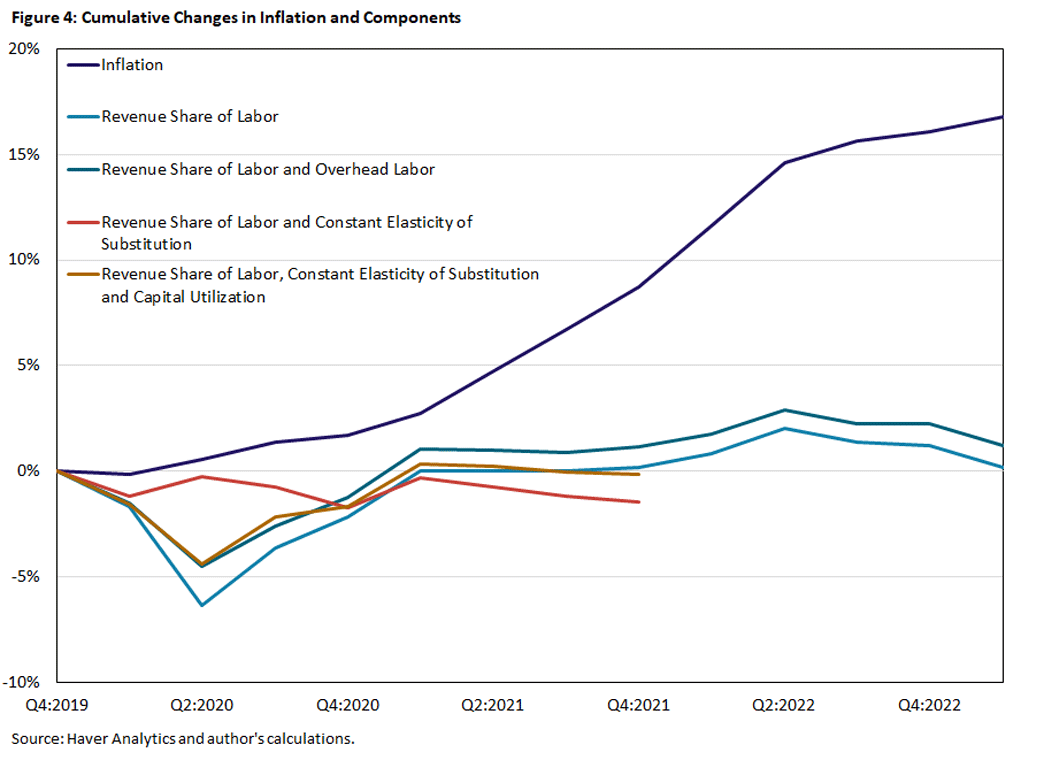
But is this approach operational for the NFCB sector? Yes, and we will now describe four ways to calculate pandemic markup changes for the NFCB sector. In Figure 4, we display the cumulative change in the NFCB sector price index since the fourth quarter of 2019 and the corresponding cumulative markup changes for our four alternative measures. As a preview, we can see that the inflation contributions of all four markup measures are rather limited.
Note that we have information on one half of the markup change expression: the revenue share of labor. It essentially is one minus the GOS. But what about the labor elasticity? The simplest thing to do is to assume that the labor elasticity is constant, and therefore no changes in labor elasticity.4 We consider this our baseline measure of markup changes.
The light blue line in Figure 4 plots the cumulative changes in the baseline markup. The implied markup declines in the first half of 2020, recovers in the second half of 2020, remains relatively constant in 2021 when inflation really picked up, then finally contributes to inflation in early 2022. Overall, this measure suggests that changes in the way firms used their market power to price above marginal cost did not contribute much to cumulative inflation.
We might be concerned that not all labor compensation as measured by the labor revenue share reflects variable labor inputs. For example, if a certain amount of labor is required to just keep a firm going without actually contributing to additional output (call it "overhead labor"), then the measured revenue share would overstate the revenue share of variable labor. We would need to adjust the labor revenue share for the presence of this overhead labor. As a first pass, assume that overhead labor and variable labor get paid the same wage, and consider the share of non-supervisory and production workers in total nonfarm business employment as the variable labor share.
The dark blue line in Figure 4 plots the thus-corrected cumulative markup, still assuming a constant labor elasticity. The cumulative markup change with the overhead-labor correction is uniformly about 1 percentage point higher than the baseline, but the qualitative behavior is otherwise very much the same.
To talk about changes in the labor elasticity, we need to impose additional structure on the production function. Again, we follow the authors of the 2020 paper and assume that GVA is produced using two inputs (labor and capital) with a particular functional form (a constant-elasticity-of-substitution production function, to be technical). For this production function, the labor elasticity of output now depends on the capital intensity of employment (that is, the capital-labor ratio). In other words, we need data on employment and the capital stock used in the NFCB sector.
The red line in Figure 4 plots the cumulative markup change based on the CES production function. Since 2022 capital stock data are not yet available, we don't have markup data for the last third of the sample. But we can talk about 2021 when inflation started to pick up. Note that our markup measure with a variable labor elasticity is less volatile than the previous markup measures, especially in 2020. Overall, though, markup changes did not contribute to inflation. In fact, changes of markups consistently reduced inflation.
Finally, similar to labor, we might think that the measured capital stock itself does not cover all the input variation coming from the capital input. After all, we can change the service flow from the given capital stock by using it more or less intensively. For our last case, we therefore add variable capital utilization to our calculations of labor elasticities. In particular, we use the utilization series from the Federal Reserve Bank of San Francisco, which is constructed for the nonfarm business sector and incorporates utilization variation of capital and labor. So, it's not perfect, but it again gives a first approximation.
The brown line in Figure 4 plots the cumulative markup based on the parameterized CES production function, allowing for variable capital utilization. As we can see, utilization variation reintroduces markup volatility in 2020. In fact, markup changes with variable labor elasticity and variable capital utilization look remarkably similar to our baseline case with a constant labor elasticity. But overall, markup changes also did not contribute much to inflation according to this measure, especially in 2021 when inflation picked up.
Conclusion
Inflation in the U.S. and other developed economies increased drastically in the years following the 2020 pandemic. We discussed two methods to calculate the contributions of increasing profit rates to inflation in the U.S. NFCB sector in the years 2020 to 2022.
The first method attributes price changes to changes in the income components of the sector's GVA, in particular, the contributions from the GOS or NOS as a measure of profits. We have argued that this method seems ill suited to account for the role of profit rate changes because of conceptual problems.
The second method constructs measures of price-cost markups using basic economic concepts which have been applied previously in the literature. We find that changes in profit-taking as reflected in the behavior of markups did not contribute much to inflation.
I thank Alex Wolman and Chen Yeh for comments and David Ramachandran for research assistance.
Andreas Hornstein is a senior advisor in the Research Department at the Federal Reserve Bank of Richmond.
See, for example, the 2023 articles "To Fight Stickier Inflation, Governments Take Aim at Corporate Profits," "'Greedflation' Is the European Central Bank's Latest Headache Amid Fears It's the Key Culprit for Price Hikes" or "Corporate Profits Have Contributed Disproportionately to Inflation. How Should Policymakers Respond?"
My Richmond Fed colleague Chen Yeh surveyed some of this literature in his 2023 article "How Costly Is Rising Market Power for the U.S. Economy?"
See, for example, the 2023 paper "Sellers' Inflation, Profits and Conflict: Why Can Large Firms Hike Prices in an Emergency?"
This assumption is actually not that unreasonable in that it would reflect a Cobb-Douglas production function, a concept that is usually seen as giving a reasonable first approximation of production structures.
To cite this Economic Brief, please use the following format: Hornstein, Andreas. (November 2023) "Profits and Inflation in the Time of COVID." Federal Reserve Bank of Richmond Economic Brief, No. 23-38.
This article may be photocopied or reprinted in its entirety. Please credit the author, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.
Views expressed in this article are those of the author and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.
Receive a notification when Economic Brief is posted online.