How Likely Is a Return to the Zero Lower Bound?
The likelihood of returning to near-zero interest rates is relevant to policymakers in considering the path of future interest rates. At the zero lower bound, the Fed can no longer lower rates and thus can respond to a contraction only through alternative policy measures, such as quantitative easing. Recent research at the Richmond Fed has used repeated simulations of the U.S. economy to estimate the probability of such an occurrence over the next ten years. The estimated probability of returning to the zero lower bound one or more times during this period is approximately one chance in four.
The short-term nominal interest rate — the primary tool of central banks when conducting monetary policy — is generally believed to have a lower bound at a rate of zero or near-zero. The Federal Reserve held the federal funds rate at this zero lower bound, as it is commonly known, for an extended period during and after the Great Recession, which began in the fourth quarter of 2007.1 In such circumstances, the central bank can provide further stimulus only with unconventional monetary policies, such as the Fed's large-scale asset purchases ("quantitative easing"). While the asset purchase programs may have been effective in stimulating the economy, they were politically unpopular and are thought by some to have created risks to monetary policy independence. It is reasonable to conjecture that some future recession will cause the Fed to reach the zero lower bound again and resort to unconventional policies — but how soon? What is the probability of the Fed having to do so in, say, the next five or ten years?
One reason why such questions are policy-relevant is that nominal interest rates have remained low for a sustained period during the present economic expansion. Although nominal rates have increased steadily since the Fed ended its policy of maintaining a near-zero federal funds rate, which was in place from December 2008 to December 2015, they are still low from a historical perspective.2 In addition, there is some evidence that structural factors, such as demography and a slowing of technological advances, have led to a decline in real interest rates, which are a component of nominal rates.3 More than usual, then, a slow pace of rate increases in the future could affect whether rates will be high enough at the time of the next contraction that the Fed can provide the desired stimulus without returning to the zero lower bound — that is, whether the Fed will have moved interest rates to a sufficient distance from zero. At the same time, overly aggressive rate increases by the Fed could lead to the conditions for a contraction to occur in the first place. Thus, to inform interest rate policy, it is desirable for policymakers to have an estimate of the likelihood of interest rates returning to the zero lower bound in coming years.
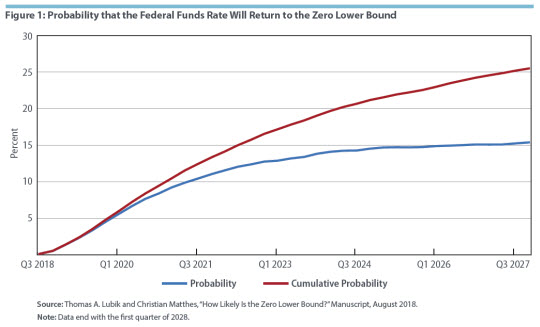
Two of the authors of this Economic Brief, Lubik and Matthes, have used an econometric forecasting model to estimate the probability of the federal funds rate reaching the zero lower bound in any given quarter from the third quarter of 2018 through the first quarter of 2028.4 On the basis of historical patterns captured with this model, they estimate that the probability is initially close to zero and increases over time to a little more than 15 percent in 2028. Cumulatively, the probability of reaching the zero lower bound sometime over the ten-year period is one chance in four. (See Figure 1.)
Generating the Interest Rate Simulations
The researchers employed a model of the U.S. economy that they developed for forecasting and policy analysis and which is used at the Richmond Fed to develop the Bank's national economic forecasts in connection with preparations for Federal Open Market Committee meetings.5 It is a vector autoregression (VAR) model, a type of model that does not require a detailed framework of economic theory to produce estimates. More specifically, it is a time-varying parameter VAR (TVP-VAR), a methodology that is exceptionally flexible in that it can handle nonlinear behavior in the data — for example, the responses of economic variables to changes in interest rates (as some of the variables behave differently than normal when rates are at or near zero).6
Another reason TVP-VARs have proved useful for forecasting is that they allow researchers to distinguish between structural or long-lasting changes in the economy and shorter-term fluctuations that are driven by changes in the volatility of shocks hitting the economy. The main drawback of TVP-VARs is that the degree of uncertainty in their forecasts is generally higher.
Lubik and Matthes began by estimating the TVP-VAR model over the full sample from 1961 to 2018 for quarterly data on real GDP, inflation (personal consumption expenditures inflation), and the federal funds rate. They then used the model's estimated coefficients to produce forecasts over a ten-year horizon. The researchers generated multiple simulations of the shocks hitting the economy over the ten-year period and recorded their effects on macroeconomic variables for each quarter. The result of this process was a distribution of likely outcomes for each quarter.
The researchers measured the probability of hitting the zero lower bound in two ways. First, they measured the probability that the federal funds rate forecast would be at or below zero in a given quarter. They did so by counting, for each quarter in the ten-year period, how many times the federal funds rate was at or below zero in that quarter in all the simulated trajectories and dividing by the total number of simulated trajectories. Second, for each quarter, they measured the cumulative share of simulated trajectories in which the federal funds rate reached the zero lower bound in or before that quarter.
The caveats that apply to any forecasting model apply to these zero-lower-bound probabilities, as well: namely, that the estimated model must be a good descriptor of the underlying data and that forecasts are freighted with greater uncertainty as the time horizon becomes longer.7
The Simulation Results
Figure 1 shows both measures of zero-lower-bound probability, with the blue line representing the probability of hitting the zero lower bound in a given quarter and the red line representing the cumulative probability. As noted, the probability starts at essentially zero and gradually rises toward a long-run level of 15.4 percent. From a policymaker's perspective, this indicates that there is a 15.4 percent chance that the economy will be in a situation in 2028 where the federal funds rate is again constrained at zero, given the estimated historical patterns of shocks when extrapolated forward.
The cumulative probabilities show a similar pattern, starting virtually at zero and rising to a long-run level of 25.5 percent. In other words, by 2028, roughly one-fourth of all forecasted trajectories of the federal funds rate hit the zero lower bound at least once.
Estimates of zero-lower-bound probabilities, as discussed in this article, are useful tools for policymakers to consider in assessing the likelihood that the key policy rate for the Fed will reach an effective floor, in which case the Fed may conclude that it must resort to unconventional policy measures again, as it did in the aftermath of the Great Recession.8
Thomas A. Lubik is a senior advisor, Christian Matthes is a senior economist, and David A. Price is senior editor in the Research Department of the Federal Reserve Bank of Richmond.
The experience of other major central banks, such as the European Central Bank and the Bank of Japan, shows that the effective lower bound on nominal interest rates can be less than zero — in other words, monetary policy may be able to achieve negative interest rates. See Tim Sablik, "Subzero Interest," Econ Focus, First Quarter 2016, pp. 3–5. It is generally believed, however, that the Fed would be unlikely to consider negative policy rates and thus that the effective lower bound is zero in the United States.
The history of the FOMC's target federal funds rate or range since 2003 is set out on the Board of Governors of the Federal Reserve System website at https://www.federalreserve.gov/monetarypolicy/openmarket.htm. Data for additional years back to 1990 are available at https://www.federalreserve.gov/monetarypolicy/openmarket_archive.htm.
Kathryn Holston, Thomas Laubach, and John C. Williams, "Measuring the Natural Rate of Interest: International Trends and Determinants," Journal of International Economics, May 2017, vol. 108, supp. 1, pp. S59–S75; Thomas A. Lubik and Christian Matthes, "Calculating the Natural Rate of Interest: A Comparison of Two Alternative Approaches," Federal Reserve Bank of Richmond Economic Brief No. 15-10, October 2015.
Thomas A. Lubik and Christian Matthes, "How Likely Is the Zero Lower Bound?" Manuscript, August 2018.
Thomas A. Lubik and Christian Matthes, "Time-Varying Parameter Vector Autoregressions: Specification, Estimation, and an Application," Economic Quarterly, Fourth Quarter 2015, vol. 101, no. 4, pp. 323–352.
Thomas A. Lubik, Christian Matthes, and Andrew Owens, "Beveridge Curve Shifts and Time-Varying Parameter VARs," Economic Quarterly, Third Quarter 2016, vol. 102, no. 3, pp. 197–223; Fabio Canova, Filippo Ferroni, and Christian Matthes, "Approximating Time Varying Structural Models with Time Invariant Structures," Federal Reserve Bank of Richmond Working Paper No. 15-10, September 2015.
Lubik and Matthes validated the model with an out-of-sample exercise, which is detailed in Lubik and Matthes (2018).
Perhaps the closest prior research is Hess Chung, Jean-Philippe Laforte, David Reifschneider, and John C. Williams, "Have We Underestimated the Likelihood and Severity of Zero Lower Bound Events?" Journal of Money, Credit and Banking, February 2012, supplement to vol. 44, no. 1, pp. 47–82. These researchers employed several forecasting models used in the policy process, such as the Fed's own large-scale macroeconometric model FRB/US, two canonical New Keynesian dynamic stochastic general equilibrium (DSGE) models, as well as a TVP-VAR closely related to the one used here. In a similar simulation exercise, they estimated models based on data up to and including the fourth quarter of 2007. None of the models, perhaps surprisingly least of all the TVP-VAR, included the zero lower bound in their 95 percent coverage region, which echoes some of Lubik and Matthes's findings. But they focused on this one base year only, while Lubik and Matthes computed probabilities for forty quarters out and also conducted a model validation exercise. Another closely related article is Michael T. Kiley and John M. Roberts, "Monetary Policy in a Low Interest Rate World," Brookings Papers on Economic Activity, Spring 2017, pp. 317–372. Kiley and Roberts used both FRB/US and a standard DSGE model often used in the Fed policy process. They found that the probability of hitting the zero lower bound is small, reaching at most 20 percent for levels of the natural rate of interest at 3 percent, which is consistent with the natural rate forecast embedded in Lubik and Matthes's model.
This article may be photocopied or reprinted in its entirety. Please credit the authors, source, and the Federal Reserve Bank of Richmond and include the italicized statement below.
Views expressed in this article are those of the authors and not necessarily those of the Federal Reserve Bank of Richmond or the Federal Reserve System.
Receive a notification when Economic Brief is posted online.